Strona 1 z 3
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 15:40
autor: Sylwek
Udowodnij, że jeżeli trójkąt jest ostrokątny, to jego obwód jest większy od podwojonej średnicy okręgu opisanego.
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:10
autor: Swistak
Według mnie należałoby tu skorzystać zapewne z faktu, że każda średnica okręgu opisanego przecina ten trójkąt.
EDIT:
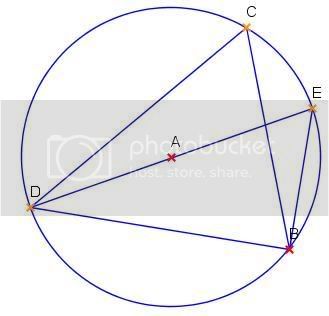
- AU
- GeoNextokrg.jpg (12.61 KiB) Przejrzano 378 razy
Jak udowodnisz, że |DC|+|BC|>|DE|+|EB| to będzie po ptakach.
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:17
autor: Piotr Rutkowski
Mógłbyś rozwinąć, bo ja tego nie widzę...
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:33
autor: binaj
mam pewien pomysł, nie wiem tylko czy dobry:
oznaczmy boki trójkąta przez a,b,c
środek okręgu opisanego O
OA=OB=OC=R
teza:
a+b+c>4R
ponieważ trójkąty ABO,ACO,BCO są rozwartokątne to:
\(\displaystyle{ a ^{2} > R ^{2}+R ^{2} = 2R ^{2}}\)
\(\displaystyle{ b^{2} > 2R ^{2}}\)
\(\displaystyle{ c^{2} > 2R ^{2}}\)
\(\displaystyle{ \sqrt \frac{{a ^{2}+b ^{2}+c ^{2}}}{3} \geqslant \frac{a+b+c}{3}}\)
\(\displaystyle{ \sqrt{ \frac{6R ^{2} }{3} } = \sqrt{2}R}\)
\(\displaystyle{ \sqrt{2}R > \frac{4}{3} R}\)
\(\displaystyle{ \sqrt{2}R \geqslant \frac{a+b+c}{3}}\)
z tego wynika:
\(\displaystyle{ \frac{a+b+c}{3}>\frac{4}{3} R}\)
\(\displaystyle{ a+b+c>4R}\)
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:39
autor: Swistak
W swoim rozumowaniu przyjąłeś, że każdy kąt jest większy od 45 stopni, bo środkowy oparty na tym samym łuku jest rozwarty. I w dodatku przejście z 3 do 2 nierówności od końca jest po prostu złe.
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:41
autor: Piotr Rutkowski
Niestety panowie obaj jesteście w błędzie. Po pierwsze Swistak, jestem ciekaw jak z Twojej nierówności ma wypływać teza zadania. Po drugie binaj skąd wziąłeś te wszystkie założenia do swojego rozwiązania? (tak w ogóle to próbowałeś udowodnić silniejszą (i nieprawdziwą) tezę)
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:46
autor: binaj
polskimisiek pisze:(tak w ogóle to próbowałeś udowodnić silniejszą (i nieprawdziwą) tezę)

chodzi o a+b+c>4R?? czy coś innego?
Swistak pisze:W swoim rozumowaniu przyjąłeś, że każdy kąt jest większy od 45 stopni
sorki mój błąd, mój rysunek mnie źle naprowadził
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:47
autor: Swistak
OK już tłumaczę.
Przyjmijmy |DC|=a, |BC|=b, |DB|=c, |DE|=d i |EB|=e.
Jeżeli a+b>d+e to a+b+c>d+e+c>d+d=2d. Oczywiście e+c>d z nierówności trójkąta.
[ Dodano: 16 Marca 2008, 16:49 ]
binaj pisze:polskimisiek pisze:(tak w ogóle to próbowałeś udowodnić silniejszą (i nieprawdziwą) tezę)

chodzi o a+b+c>4R?? czy coś innego?
Chodzi o to, że "udowodniłeś", że
\(\displaystyle{ a+b+c qslant 3\sqrt{2}}\).
P.S. To mój 100 post .
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:51
autor: binaj
ok, rozumiem już nie będę pisał głupot
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 16:54
autor: Swistak
binaj pisze:ok, rozumiem już nie będę pisał głupot

No to czekamy na coś mądrego

.
EDIT: Udowadniajcie, któreś z tych:
\(\displaystyle{ a+b>d+e \\ a^{2}+b^{2}>d^{2}+e^{2}}\)
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 17:08
autor: Wasilewski
Albo udowodnijcie:
\(\displaystyle{ P > \frac{abc}{a + b + c}}\)
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 17:09
autor: TomciO
Tw. sinusow natychmiast zalatwia sprawe.
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 17:34
autor: Sylwek
Poszło za pomocą pierwszej wskazówki
Świstaka 
, już tłumaczę: niech
\(\displaystyle{ X}\) to punkt przecięcia
\(\displaystyle{ BC}\) i
\(\displaystyle{ DE}\). No i standard w takich zadaniach: łatwo zauważyć, że
\(\displaystyle{ \Delta DCX \sim \Delta BEX}\), więc:
(1):
\(\displaystyle{ \frac{DC+CX}{DX}=\frac{BE+EX}{BX} \iff \frac{DC+CX-DX}{DX}=\frac{BE+EX-BX}{BX}}\)
Ale LEMAT:
\(\displaystyle{ DX>DA \Rightarrow DX>BX}\) (dość prosto to można udowodnić, jako że
\(\displaystyle{ BA}\) to środkowa trójkąta prostokątnego
\(\displaystyle{ \Delta DBE}\), jedna nierówność trójkąta i gotowe)
Z LEMATU i (1):
\(\displaystyle{ DX>BX \Rightarrow DC+CX-DX>BE+EX-BX}\), czyli:
(2):
\(\displaystyle{ DC+CX+BX>BE+EX+DX \iff DC+BC>BE+DE}\)
No więc:
\(\displaystyle{ DC+BC+DB>DE+(BE+BD)>DE+DE=2DE}\)
Ostatnia nierówność z nierówności trójkąta
Nie odpowiadam za literówki, gdyż miałem inne oznaczenia u siebie na rysunku, a tu musiałem troszkę pozmieniać, mimo wszystko powinno być dobrze
Jak ktoś ma inny sposób, to może zaprezentować, bo widzę paru chętnych napisało posty powyżej
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 17:45
autor: Swistak
Już chyba mam. Zrobiłem to na wektorach.
Oczywiście
\(\displaystyle{ P _{DCB} \geqslant P_{BDE}}\), a z tego i z wzoru na pole trojkąta z iloczynem dwóch boków i sinusem kąta wynika i z tego, że mamy tam 2 katy wpisane oparte na c wynika, że ab>de
\(\displaystyle{ (\vec{a} + \vec{b})^{2}= \vec{c}^{2}= ( \vec{d} + \vec{e})^{2}}\)
Nie znam się do końca na tym jak to się pisze i gdzie się wstawia te kwadraty, ale to leci tak:
\(\displaystyle{ \vec{a} ^{2} +2 \vec{a} \vec{b} + \vec{b} ^2=\vec{d} ^{2} +2 \vec{d} \vec{e} + \vec{e} ^2 \\
\vec{a} ^{2} + \vec{b} ^2=\vec{d} ^{2} +2 \vec{d} \vec{e} + \vec{e} ^2 - 2 \vec{a} \vec{b} > \vec{d} ^{2}+\vec{e} ^{2}}\), bo tam są 2 kąty wpisane oparte na c i ab>de.
Skoro
\(\displaystyle{ \vec{a} ^{2} + \vec{b} ^2>\vec{d} ^{2}+\vec{e} ^{2}}\) to też
\(\displaystyle{ a^{2}+b^{2}>d^{2}+e^{2} \\
(a+b)^{2}=a^{2}+b^{2}+2ab>d^{2}+e^{2}+2ed=(e+d)^{2}}\)
\(\displaystyle{ a+b>d+e}\)
\(\displaystyle{ a+b+c>d+e+c>d+d>2d}\)
c.b.d.u.
Możliwe, ze w moim rozumowaniu jest błąd, ale w wektorach jestem dość zielony, ale wydaje mi się, że mam dobrze

.
[ Dodano: 16 Marca 2008, 18:05 ]
Mam kolejny dowód, który jest trochę podobny do dowodu Sylwka, możliwe, że to nawet to samo, ale zapewniam, ze powstał całkowicie niezależnie (najpierw zrobiłem swój, potem przeczytałem Sylwka

)
Przyjmijmy skalę podobieństwa trójkątów DCX i BCX jako k (gdzie CDX jest większy)
Z nierówności trójkąta:
\(\displaystyle{ |EB|+|EX|>|BX| \\
(|EB|+|EX|)(k-1)>|BX|(k-1) \\
|EB|(k-1)+|EX|(k-1)>|BX|(k-1) \\
|EB|k-|EB|+|EX|k-|EX|>|BX|k-|BX| \\
|EB|k+|EX|k+|BX|>|EB|+|EX|+|BX|k \\
|DC|+|CX|+|BX|>|EB|+|EX|+|DC| \\
|DC|+|CB|>|EB|+|DE|}\)
Dalszy ciąg już zapewne znacie.
[Nierówności][Planimetria] Trójkąt ostrokątny a średnia okręgu opisanego
: 16 mar 2008, o 18:13
autor: TomciO
Po zastosowaniu tw. sinusów (\(\displaystyle{ \frac{a}{\sin \alpha} = 2R}\) itd.) trzeba wykazac, ze \(\displaystyle{ \sin \alpha + \sin \beta + \sin \gamma > 1}\). A to jest jasne, bo skoro trojkat jest ostrokatny to co najmniej dwa katy sa w przedziale \(\displaystyle{ [45; 90)}\).