Strona 1 z 1
Zadanie z pochodnymi
: 12 mar 2023, o 12:45
autor: Merherri
Cześć! W sprawozdaniu muszę z wyrażenia
\(\displaystyle{ \frac{V}{V_0} = f(t)}\) (objętość/objętość początkowa w funkcji czasu) otrzymać jego pierwszą pochodną -
\(\displaystyle{ \frac{d\left( \frac{V}{V_0}\right) }{dt} = f(t)}\). Jak to zrobić?
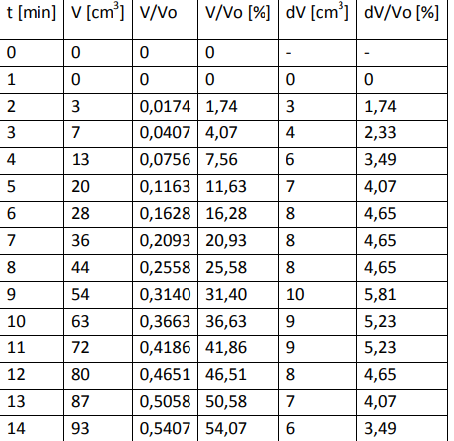
- d23244096cfa3f43gen.png (66.26 KiB) Przejrzano 503 razy
To jest przykładowa tabelka z wynikami zamieszczona w ćwiczeniu. Ja mam liczby np.
\(\displaystyle{ V=25, V_0=179,55, t=4.}\)
Re: Zadanie z pochodnymi
: 12 mar 2023, o 21:24
autor: janusz47
\(\displaystyle{ f'(t) = \frac{\frac{dV(t)}{dt}\cdot V_{0}(t) - V(t)\cdot \frac{dV_{0}(t)}{dt}}{V^2_{0}(t)} }\)
Dodano po 40 minutach 51 sekundach:
Funkcji \(\displaystyle{ f(t) }\) jest w postaci:
\(\displaystyle{ \frac{V(t)}{V_{0}(t)} \ \ V_{0}(t) \neq 0.}\)
Obliczamy wyżej jej pochodną, jako pochodną ilorazu funkcji.