Strona 1 z 1
kąt i okręgi
: 27 lis 2018, o 17:57
autor: ann_u
Okrąg \(\displaystyle{ x}\) jest styczny wewnętrznie z okręgiem \(\displaystyle{ y}\) w punkcie \(\displaystyle{ P}\). Środek \(\displaystyle{ O}\) okręgu \(\displaystyle{ y}\) lezy na zewnątrz okręgu \(\displaystyle{ x}\). Odcinek \(\displaystyle{ MN}\) jest średnicą okręgu \(\displaystyle{ y}\) , która jest styczna do okręgu \(\displaystyle{ x}\). Wiadomo że \(\displaystyle{ PM>PN}\) oraz \(\displaystyle{ PM}\) przecina \(\displaystyle{ x}\) w punkcie \(\displaystyle{ Z}\). Wyznacz miarę kat \(\displaystyle{ PMN}\), jeśli \(\displaystyle{ MZ=2PZ.}\)
Re: kąt i okręgi
: 29 lis 2018, o 14:39
autor: macik1423
Spróbuj wyznaczyć za pomocą twierdzenia Talesa na jakie długości dzieli odcinek \(\displaystyle{ OP}\) punkt przecięcia okręgu \(\displaystyle{ x}\) z tym odcinkiem. Zauważ, że odcinek \(\displaystyle{ OP}\) przechodzi przez środek okręgu \(\displaystyle{ x}\). Skorzystaj z twierdzenia o kącie środkowym i wpisanym opartym na tym samym łuku. Wykorzystaj fakt, że promień okręgu \(\displaystyle{ x}\) jest prostopadły do promienia okręgu \(\displaystyle{ y}\) w punkcie styczności oraz to że przeciwprostokątna trójkąta prostokątnego jest średnicą okręgu opisanego na tym trójkącie.
kąt i okręgi
: 29 lis 2018, o 22:57
autor: Rados
Mógłbym prosić o sprawdzenie mojego rozwiązania, bo nie jestem pewien, czy nie popełniłem błędu?
\(\displaystyle{ MZ=2PZ \newline
\angle PMN= \alpha = ? \newline \newline
\frac{PZ}{PM}= \frac{PR}{2OP} \newline \newline
PR=2OP \frac{PZ}{PM}=2OP \frac{PZ}{3PZ}= \frac{2}{3}OP \newline
\frac{ \frac{1}{2}PR}{OP- \frac{1}{2}PR}=\sin{2 \alpha } \newline
\sin{2 \alpha }=0,5 \newline
2 \alpha=30^\circ \newline
\alpha=15^\circ}\)
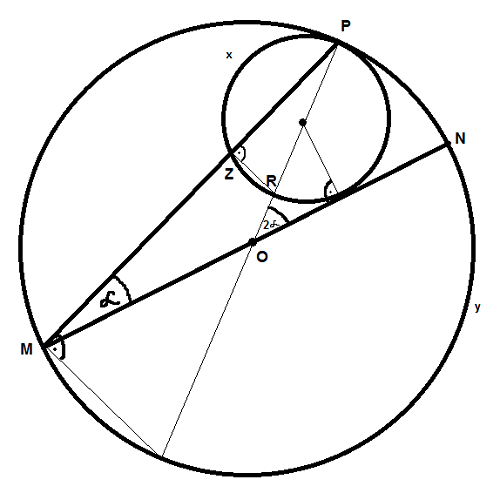
- AU
- rysunek-okrag.png (40.31 KiB) Przejrzano 298 razy
Re: kąt i okręgi
: 30 lis 2018, o 08:42
autor: macik1423
Dobrze jest.