Strona 1 z 1
Pole trójkątów
: 6 cze 2017, o 16:29
autor: Piotr998px
Witam serdecznie,
Mam parę zadań odnośnie kartkówki z pola trójkąta. Bardzo proszę o rozwiązanie krok po kroku.
Więc:
1. Oblicz pole trójkąta prostokątnego, w którym przeciwprostokątna ma długość \(\displaystyle{ 12}\), a jeden z kątów ostrych \(\displaystyle{ \alpha}\) jest taki, że \(\displaystyle{ \sin \alpha = 0,25}\).
2. Oblicz obwód trójkąta prostokątnego równoramiennego, którego \(\displaystyle{ P=18}\).
3. Dany jest trójkąt o bokach \(\displaystyle{ 6,7,8}\) i najmniejszy kąt ma miarę \(\displaystyle{ 30^\circ}\). Oblicz pole tego trójkąta.
4. Oblicz pole trójkąta równobocznego, którego wysokość wynosi \(\displaystyle{ 8}\).
Z góry dziękuję za pomoc;)
Pole trójkątów
: 6 cze 2017, o 16:54
autor: Tomuello
1.
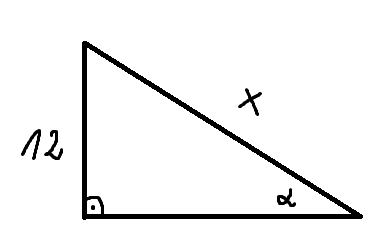
- AU
- KCtivlA.png (3.45 KiB) Przejrzano 267 razy
\(\displaystyle{ \sin \alpha = \frac{12}{x} = \frac{1}{4}}\)
Z twierdzenia pitagorasa wylicz trzeci bok i pole trójkąta.
2.
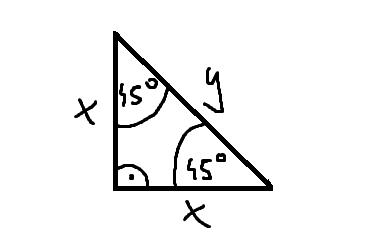
- AU
- CNqZumU.png (4.81 KiB) Przejrzano 267 razy
\(\displaystyle{ \frac{1}{2} x ^{2} =P}\)
Z pitagorasa lub własności trójkąta
\(\displaystyle{ 90,45,45 \Rightarrow y = x \sqrt{2}}\)
3.
Najkrótszy z boków leży naprzeciw najmniejszego kąta.
4.
\(\displaystyle{ a}\) - Długość boku trójkąta równobocznego
\(\displaystyle{ h}\) - Długość wysokości trójkąta równobocznego
\(\displaystyle{ P}\) - Pole trójkąta
\(\displaystyle{ h= \frac{a \sqrt{3} }{2}}\)
oraz
\(\displaystyle{ P = \frac{a ^{2} \sqrt{3} }{4}}\)
Pole trójkątów
: 6 cze 2017, o 17:00
autor: Piotr998px
Kurczę, stary dzięki wielkie za tę doraźną pomoc ale ja kompletnie nie mam o tych trójkątach pojęcia. Była by możliwość takiego dogłębniejszego rozwiązania tych zadań?
Re: Pole trójkątów
: 6 cze 2017, o 21:28
autor: Jan Kraszewski
Ale to są dogłębne rozwiązania tych zadań. Bardziej dogłębnie się nie da. Może zatem spróbuj włożyć trochę wysiłku w zrozumienie tych rozwiązań.
Np. zad 1: czy wiesz, co to jest trójkąt prostokątny, twierdzenie Pitagorasa oraz funkcje trygonometryczne w tym trójkącie? Jeśli nie, to uzupełnij braki w teorii i wróć do rozwiązania.
JK
Pole trójkątów
: 6 cze 2017, o 21:43
autor: MalinaZMelonami
Piotr998px pisze:Witam serdecznie,
1. Oblicz pole trójkąta prostokątnego, w którym przeciwprostokątna ma długość \(\displaystyle{ 12}\), a jeden z kątów ostrych \(\displaystyle{ \alpha}\) jest taki, że \(\displaystyle{ \sin \alpha = 0,25}\).
Piotr998px pisze:Witam serdecznie,
1.
Tomuello pisze:1.
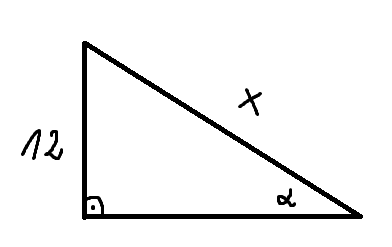
- AU
- KCtivlA.png (3.45 KiB) Przejrzano 267 razy
\(\displaystyle{ \sin \alpha = \frac{12}{x} = \frac{1}{4}}\)
Z twierdzenia pitagorasa wylicz trzeci bok i pole trójkąta.
Tu jest błąd. Przeciwprostokątna ma długość
\(\displaystyle{ 12}\) a nie przyprostokątna.
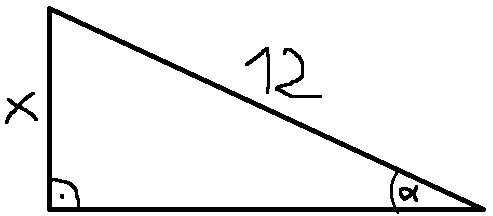
- AU
- oHxlddM.png (3.43 KiB) Przejrzano 267 razy
Wtedy:
\(\displaystyle{ \sin \alpha = \frac{x}{12} = \frac{1}{4}\\
x=3}\)
Brakujący bok liczymy z pitagorasa i liczymy pole.
Prościej się nie da.
Pole trójkątów
: 6 cze 2017, o 22:15
autor: Jan Kraszewski
MalinaZMelonami pisze:Tu jest błąd. Przeciwprostokątna ma długość \(\displaystyle{ 12}\) a nie przyprostokątna.
Czujność zawsze w cenie.
JK