Strona 1 z 8
Matura z matematyki 2016 - poziom rozszerzony
: 5 maja 2016, o 00:14
autor: Jan Kraszewski
Dyskutujemy tutaj o maturze rozszerzonej z matematyki (ale dopiero po zakończeniu egzaminu...).
JK
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 12:15
autor: Milczek
Było łatwe, jak bede w domu napisze więcej.-- 9 maja 2016, o 11:17 --Ps. Ale podchwytliwe
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 12:53
autor: AndrzejK
Wg mnie była dość trudna, znacznie trudniejsza od zeszłorocznej. Ale przynajmniej wzięli uwagi do serca i wychodziły względnie normalne wyniki.
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:00
autor: Janpostal
Zadania były trudne, \(\displaystyle{ 99%}\) siedziało do samego końca non stop coś licząc w tym ja. Dowody były niebanalne, jednego nie rozwiązałem, tego z trójkątami i okręgami, jakby ktoś podrzucił rozwiązanie byłym wdzięczny, nikogo kogo spotkałem nie zrobił tego.
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:05
autor: Milczek
Też nie zrobiłem z okręgami ale plani nie jest moją mocną stroną , tak samo jak analityczna której nie zrobiłem.
Dla mnie była łatwa, może to tylko wrażenie bo zadania mi "podpasowały" , nie było trudnej kombinatoryki, stereometrii ani prawdopodobieństwa.
Lecz jak napisałem , może tak mi się tylko wydaje, przy przepisywaniu zamkniętych zmieniłem trzy odpowiedzi na bardziej poprawne, oby z pozostałymi tak nie było.
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:06
autor: mint18
W plani trzeba było dorysować jedną dwusieczną, pobawić się trochę kątami i twierdzeniem o odcinkach stycznych. Jak odpowiedzieliście w zadaniui z ciągiem zbieżnym?
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:08
autor: Milczek
\(\displaystyle{ 186}\) chyba , albo \(\displaystyle{ 187}\) , ważna była informacja że każdy wyraz jest dodatni więc \(\displaystyle{ q\ge 0}\)
-- 9 maja 2016, o 12:15 --
bo w innym wypadku nie będzie najmniejszej liczby całkowitej, a skoro o taką prosili w poleceniu to zbiór musi być ograniczony z dołu.
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:18
autor: Drone
Dowód przeprowadziłem śmieszną i okrężną drogą (możliwe, że błędnie bo przyjąłem za oczywiste równość pewnych odcinków na przekątnej) mianowicie najpierw napisałem, że część tych odcinków zawiera się w odległości promienia przez co odjąłem promień od nich, dalej jeszcze jakiś odcinek od obu odjąłem i wyszły mi \(\displaystyle{ 2}\) trójkąty przystające (najpierw wyszło, że podobne) z czego wynikało, że ich boki są równe (a jeden z boków był ostatnią częścią odcinka).
W ciągu zbieżnym najmniejszy wyraz wyszedł mi \(\displaystyle{ 187}\).
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:20
autor: AndrzejK
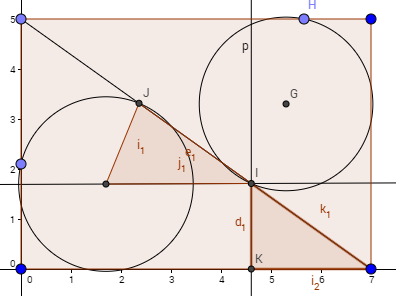
- AU
- jG4bDEW.png (20.21 KiB) Przejrzano 448 razy
Te dwa trójkąty są przystające. I dalej było już b. łatwo.
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:22
autor: Milczek
A że jestem bardzo zadowolony z tego co wypisałem składam podziękowania osobom o nickach w ukrytej części.
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:32
autor: shreder221
Nie była jakaś strasznie trudna, już prędzej średnio łatwa. Ale to nie był mój dzień więc nie spodziewam się więcej niż 60% ;( Nie mogłem się skupić, nad prostymi zadaniami i siedziałem nad nimi znacznie dłużej niż powinienem. Jak się pojawią wyniki to więcej konkretów będzie
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:33
autor: AndrzejK
Ile wyszły współrzędne punktów \(\displaystyle{ C}\) i \(\displaystyle{ D}\) w zadaniu z czworokątem wpisanym w okrąg, analityczna?
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:47
autor: vicossess
O ile nie machnąłem się w obliczeniach, to \(\displaystyle{ D = \left( 6,2 \right) , C = \left( \frac{8}{3}, \frac{14}{3} \right)}\) czy jakoś tak.
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:48
autor: AndrzejK
Oh, to super. Mam tak samo, więc jak machnęliśmy się w obliczeniach, to razem
Matura z matematyki 2016 - poziom rozszerzony
: 9 maja 2016, o 13:49
autor: shiftry123
vicossess pisze:O ile nie machnąłem się w obliczeniach, to \(\displaystyle{ D =(6,2), C = ( \frac{8}{3}, \frac{14}{3})}\) czy jakoś tak.
Mam to samo, więc myślę, że jest to prawidłowy wynik.