Matematyka.pl

Rozwiąż równanie:
||||x+2|+2|+2|+2| = 8
Z góry dziękuję!!

|||x+2|+2|+2|+2 = 8 lub |||x+2|+2|+2|+2 = - 8
Druga opcja oczywiście odpada pozostaje więc:
|||x+2|+2|+2| = 6 => ||x+2|+2|+2 = 6 lub ||x+2|+2|+2 = -6
Znowu druga możliwość odpada, czyli zostaje:
||x+2|+2| = 4 => |x+2|+2 = 4 lub |x+2|+2 = -4
Drugie rozwiązanie znowu odpada, czyli
|x+2| = 2 => x+2 = 2 lub x+2 = -2 => x = 0 lub x = -4

||||x+2|+2|+2|+2| =|x+2|+2 =8

mol_ksiazkowy, ||||x+2|+2|+2|+2| = |x+2|+6

Mógłbyś mi uzasadnić dlaczego niektóre opcje odpadają. Dla mnie niestety nie jest to takie oczywiste.

\(\displaystyle{ \bigwedge\limits_{a\in R} |a| q 0}\)
Czyli wartość bezwzględna z liczby rzeczywistej musi być zawsze nieujemna.

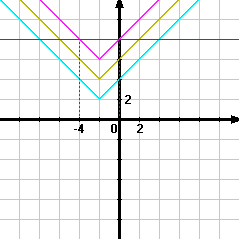
Rozwiązanie graficzne:

\(\displaystyle{ f(x)=||||x+2|+2|+2|+2|=8}\)
•\(\displaystyle{ g_1(x)=|x+2|+2}\)
•\(\displaystyle{ g_2(x)=|g_1(x)|}\)
•\(\displaystyle{ g_3(x)=g_2(x)+2}\)
•\(\displaystyle{ g_4(x)=|g_3(x)|}\)
•\(\displaystyle{ g_5(x)=g_4(x)+2}\)
•\(\displaystyle{ f(x)=|g_5(x)|}\)
•\(\displaystyle{ y=8}\)

[/url]

\(\displaystyle{ x\in\{-4,0\}}\)