Strona 1 z 1
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 21:59
autor: pjetagoras
\(\displaystyle{ 2^{x} \left( x ^{2}-1 \right) = -1}\)
rysuję wykresy lewej i prawej strony (po przekształceniu, tj. dzielę obie strony przez \(\displaystyle{ 2 ^{x}}\)) zawsze wychodzi mi, że jest tylko jedno rozwiązanie (z wykresu), w odpowiedziach są dwa rozwiązania, może mi ktoś wytłumaczyć co robię źle?
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 22:00
autor: major37
Narysuj wykres \(\displaystyle{ 2 ^{x}}\) oraz \(\displaystyle{ \frac{-1}{x ^{2}-1 }}\)
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 22:05
autor: pjetagoras
problem w tym, że nie potrafię narysować wykresu funkcji \(\displaystyle{ \frac{-1}{ x^{2}-1 }}\) gdyż nie mieliśmy nigdy takich funkcji wymiernych, nasz program kończy się jedynie na prostych tj. homograficznych, jak zrobić to inaczej?
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 22:13
autor: piasek101
\(\displaystyle{ y=x^2-1}\) oraz \(\displaystyle{ y=-2^{-x}}\) (są dwa rozwiązania, ale jedno ,,nieładne")
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 22:15
autor: pjetagoras
nie rozumiem, mnie uczono, że rozwiązanie będzie tam gdzie te dwie funkcje na wykresie się przetną a jest tylko jeden taki punkt, o co chodzi z tym "nieładne"?
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 22:24
autor: piasek101
Są dwa punkty przecięcia.
Nieładny - bo na wykresie widoczne - a co do wyznaczenia (obliczenia) wietrzę kłopoty - chociaż na razie nie próbowałem.
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 23:04
autor: major37
Ale trzeba tylko wyznaczyć liczbe rozwiązań a nie same rozwiązania.
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 23:15
autor: pjetagoras
jak dwa punkty przecięcia?? jest tylko jeden, parabola ma ramiona do góry, a krzywa wykładnicza leży w III i IV ćwiartce, jedynie punkt \(\displaystyle{ \left\{ 0,1\right\}}\) jest punktem wspólnym
zbadaj liczbę rozwiązań
: 12 kwie 2012, o 23:19
autor: anna_
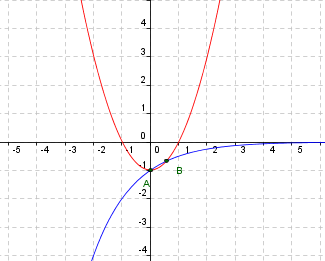
- AU
- 3dcb1cb4119c4132.png (10.32 KiB) Przejrzano 110 razy
[/url]