Strona 1 z 2
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 11:57
autor: afrolook
Wyznaczyć pierwiastki z liczby zespolonej \(\displaystyle{ \sqrt[4]{i}}\)
Z liczby bym jeszcze potrafiła, ale jak to zrobić z "i"?
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 12:07
autor: Ewa 20
Zapisz \(\displaystyle{ i}\) w postaci trygonometrycznej a potem skorzystaj z wzoru de Moivre'a.
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 12:45
autor: afrolook
no i tu pojawia się problem, bo z liczbami to jeszcze jest pół biedy, ale nie wiem jak zrobić to w postaci trygonometrycznej.
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 12:58
autor: green_01
Postac trygonometryczne:
|z| = 1 bo \(\displaystyle{ \sqrt{1^2 + 0}}\)
cos = 0;
sin = 1;
kąt : \(\displaystyle{ \pi/2}\)
Postac tryg. :
\(\displaystyle{ (cos \pi/2 + isin \pi/2)}\)
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 12:59
autor: Ewa 20
Wzór znajdziesz tutaj:
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:03
autor: afrolook
Dziękuję green
Ewa 20 wzory mam ale z i mam zawsze problem, tak samo jak z "e" he he
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:04
autor: green_01
Przy potegach uzywajac postaci tryg. i wzoru Moivre patrzysz tylko na liczbe przy "i" a jak jej nie ma to jest 0. Tyle...
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:04
autor: miodzio1988
oczywiscie green_01, wyznaczyl tylko jeden pierwiastek. jeszcze 3 zostaly.
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:12
autor: green_01
BLAD!!! Na pierwiastki jest inny wzor ;/
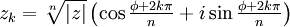
- AU
- 19e6c3c90b7e7309158bc662f7092e08.png (1.35 KiB) Przejrzano 246 razy
Czyli:
\(\displaystyle{ W_{0} = 1(cos \pi/8 +isin \pi/8)}\)-> pierwszy pierwiastek.
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:25
autor: afrolook
trzy?
a możecie mi w tym pomóc?
PRzedstawić liczbę zespoloną w postaci trygonometrycznej z= - 5 + \(\displaystyle{ 5\sqrt{3}i}\)
Dla z= - 5 + \(\displaystyle{ 5\sqrt{3}i}\) mamy
r=\(\displaystyle{ 2\sqrt{10}}\)
r=((\(\displaystyle{ -5)^{2}}\) + \(\displaystyle{ (5\sqrt{3}i)^{2}}\) = 25 + 5 * 3 = 40 = \(\displaystyle{ 2\sqrt{10}}\)
cos = \(\displaystyle{ \frac{-5}{2 \sqrt{10} }}\)
sin = \(\displaystyle{ \frac{5 \sqrt{3} }{2 \sqrt{10} }}\)
Zatem
-5 + \(\displaystyle{ 5\sqrt{3}i}\) = ( cos \(\displaystyle{ \frac{-5}{2 \sqrt{10} }}\) + i sin \(\displaystyle{ \frac{5 \sqrt{3} }{2 \sqrt{10} }}\) )
[ Dodano: 3 Stycznia 2009, 13:27 ]
hmm, czyli jak ma wyglądać green ten pierwszy przykład?
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:38
autor: green_01
Tam powinno byc 25 + 75. Bo \(\displaystyle{ 5^2+5\sqrt{3} =5^2 + 5^2 * \sqrt{3}^2 = 25 + 25*3 =100}\)
I wtedy pierwiastek wyniesie 10 i sie ladnie skroci, czyli
cos = -1/2
sin = \(\displaystyle{ 5\sqrt{3} /10 = \sqrt{3}/2}\)
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:51
autor: afrolook
Czyli dalej powinno być tak, że
cos = \(\displaystyle{ \frac{-5}{100}}\) = \(\displaystyle{ \frac{-1}{20}}\)
i sin = \(\displaystyle{ \frac{5 \sqrt{3} }{100}}\) = \(\displaystyle{ \frac{ \sqrt{3} }{20}}\)
Zatem
-5 + \(\displaystyle{ 5\sqrt{3}i}\) = (cos \(\displaystyle{ \frac{-1}{20}}\) + i sin \(\displaystyle{ \frac{ \sqrt{3} }{20}}\)
Tak ma to wyglądać ostatecznie?
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 13:58
autor: green_01
Od nowa, wszystko pomyliles.
Obliczas modul a wzor na modul to \(\displaystyle{ |z|=\sqrt{x^2+y^2}}\)
x - czesc rzeczywista
y- czesc urojona , liczba ktora stoi przy "i".
|z| = \(\displaystyle{ \sqrt{5^2+(5\sqrt{3})^2} =\sqrt{5^2 + 5^2 * \sqrt{3}^2} = \sqrt{25 + 25*3} =\sqrt{100} = 10}\)
Teraz kąty:
Wzory:
cos = x/|z|
sin = y/|z|
czyli
cos = -5/10 = -1/2
sin = \(\displaystyle{ 5\sqrt{3} /10 = \sqrt{3}/2}\)
i dalej chyba wiesz...
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 14:05
autor: afrolook
Czyli dalej wygląda
Zatem -5 + \(\displaystyle{ 5\sqrt{3}i}\) = ( cos \(\displaystyle{ \frac{-1}{2}}\) + i sin \(\displaystyle{ \frac{ \sqrt{3} }{2}}\) )
?? Czy ja musze to zamienić żeby było w radianach?
Wyznaczyć pierwiast z liczby zespolonej
: 3 sty 2009, o 14:12
autor: green_01
Nie znasz wzorow!
Zapomiales o 10 przed nawiasem. Wzor na postac tryg. :
\(\displaystyle{ |z|(cos \varphi + isin \varphi ).}\)
Zamien na radiany, czyli to bedzie \(\displaystyle{ 5/6 \pi}\) bo cos jest ujemny sin dodatni.