Strona 1 z 2
Całka zespolona po konturze
: 27 lis 2022, o 12:39
autor: forest99
\(\displaystyle{ \int_{C}^{} \frac{1}{(z^2-1)(z-2)} dz }\), gdzie
\(\displaystyle{ C}\) jest konturem
\(\displaystyle{ x^2 + (y-1)^2 = 1}\)
Tak wygląda kontur:
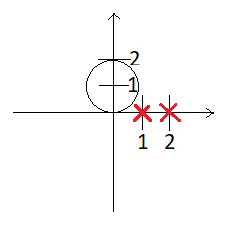
- Bez-tytu-u.png (2.14 KiB) Przejrzano 10927 razy
Obydwa punkty osobliwe (1 i 2) z niego wypadają.
\(\displaystyle{ \frac{1}{(z^2-1)(z-2)} = \frac{1}{(z-1)(z+1)(z-2)} }\)
Chyba można ją obliczyć najłatwiej za pomocą wzoru całkowego Cauchy'ego, po podzieleniu całki na dwa obszary: dk1 i dk2? To znaczy tak bym robiła, gdybym wiedziała gdzie są punkty osobliwe wewnątrz. Bo domyślam się, że tw. podstawowego Cauchy'ego tutaj nie zastosuję.
W książce Żakowskiego jest łatwiejszy przykład, w którym bierze pod uwagę jeszcze
\(\displaystyle{ i}\), ale w tym konkretnym przypadku nie wiem, jak to zrobić, ani czy w ogóle idę w dobrym kierunku.
Re: Całka zespolona po konturze
: 27 lis 2022, o 13:22
autor: janusz47
Przedstawiamy funkcję podcałkową w postaci sumy ułamków prostrych.
Parametryzujemy równanie okręgu.
Obliczamy sumę całek.
Re: Całka zespolona po konturze
: 27 lis 2022, o 13:29
autor: a4karo
Jak znasz twierdzenie o residuach, to nic nie musisz liczyć
Re: Całka zespolona po konturze
: 27 lis 2022, o 15:39
autor: forest99
Żeby obliczyć to metodą residuów, to też muszę znaleźć punkty osobliwe, a z tym mam problem w tym zadaniu
Re: Całka zespolona po konturze
: 27 lis 2022, o 15:48
autor: a4karo
Przecież punkty osobliwe są tam gdzie mianownik się zeruje.
Re: Całka zespolona po konturze
: 27 lis 2022, o 15:55
autor: forest99
Tak, tak jak w poście głównym jest napisane - to są z=1 i z=2, ale one leżą poza obszarem całkowania. A jeśli dobrze rozumiem, to żeby obliczyć metodą residuów, to tak jak we wzorze całkowym Cauchy'ego, muszę mieć punkt osobliwy wewnątrz obszaru?
Re: Całka zespolona po konturze
: 27 lis 2022, o 17:08
autor: Dasio11
forest99 pisze: 27 lis 2022, o 12:39Bo domyślam się, że tw. podstawowego Cauchy'ego tutaj nie zastosuję.
A próbowałaś?
forest99 pisze: 27 lis 2022, o 15:55tak jak w poście głównym jest napisane - to są z=1 i z=2,
I jeszcze
\(\displaystyle{ z=-1}\).
Re: Całka zespolona po konturze
: 27 lis 2022, o 18:00
autor: arek1357
A jeśli dobrze rozumiem, to żeby obliczyć metodą residuów, to tak jak we wzorze całkowym Cauchy'ego, muszę mieć punkt osobliwy wewnątrz obszaru?
To źle rozumiesz///
Re: Całka zespolona po konturze
: 27 lis 2022, o 18:03
autor: janusz47
Z treści zadania wynika, że kontur \(\displaystyle{ C = |z-i| =1 }\) jest okręgiem jednostkowym o środku w punkcie \(\displaystyle{ S=(0, i) }\)
Funkcja podcałkowa \(\displaystyle{ f(z) = \frac{1}{ (z+1)(z-1)(z-2)} }\) jest analityczna z wyjątkiem punktów \(\displaystyle{ \ \ z_{1}=(-1,0), \ \ z_{2}= (1, 0), z_{3}= (0,2).}\)
Kontur \(\displaystyle{ C }\) może być ściągnięty do punktów \(\displaystyle{ z_{1}, \ \ z_{2}, \ \ z_{3}. }\)
\(\displaystyle{ \int_{C} \frac{1}{(z+1)(z-1)(z-2)} = \int_{\Gamma} \frac{1}{6(z+1)} - \int_{\Gamma} \frac{1}{2(z-1)} + \int_{\Gamma}\frac{1}{3(z-2)}. }\)
Na podstawie twierdzenia Cauchy:
\(\displaystyle{ \int_{\Gamma} \frac{dz}{z-a} = \begin{cases} 0, \ \ a\in \Gamma \\ 2\pi i, \ \ a \notin \Gamma. \end{cases} }\)
Re: Całka zespolona po konturze
: 27 lis 2022, o 18:28
autor: a4karo
forest99 pisze: 27 lis 2022, o 15:55
a4karo pisze: 27 lis 2022, o 15:48
Przecież punkty osobliwe są tam gdzie mianownik się zeruje.
Tak, tak jak w poście głównym jest napisane - to są z=1 i z=2, ale one leżą poza obszarem całkowania. A jeśli dobrze rozumiem, to żeby obliczyć metodą residuów, to tak jak we wzorze całkowym Cauchy'ego, muszę mieć punkt osobliwy wewnątrz obszaru?
Przeczytaj twierdzenie. Jak we wnętrzu obszaru nie ma residuów, to zadanie staje się banalnie proste.
Dla zdrowia psychicznego nie czytaj tego co pisze janusz47.
Re: Całka zespolona po konturze
: 27 lis 2022, o 18:40
autor: arek1357
Kontur C może być ściągnięty do punktów \(\displaystyle{ z_{1}, z_{2}, z_{3}}\)
Jak można tego dokonać?
Dodano po 3 minutach 13 sekundach:
A co to za krzywa
\(\displaystyle{ \Gamma}\)
Re: Całka zespolona po konturze
: 27 lis 2022, o 23:34
autor: janusz47
Przyjmuje się, że kontur \(\displaystyle{ \Gamma }\) jest to kontur skierowany dodatnio (przeciwnie do ruchu wskazówek zegara) nie zawierający biegunów funkcji podcałkowej.
\(\displaystyle{ \int_{C} \frac{1}{(z+1)(z-1)(z-2)} = \int_{C} \frac{1}{6(z+1)} - \int_{C} \frac{1}{2(z-1)} + \int_{C}\frac{1}{3(z-2)}= \frac{1}{6}2\pi i-\frac{1}{2}2\pi i + \frac{1}{3}2\pi i = 0.}\)
Obliczając każdą z całek po konturze \(\displaystyle{ \Gamma = C }\) otrzymujemy kolejno:
\(\displaystyle{ \frac{1}{6} \int_{C}\frac{1}{z+1} dz = \int_{0}^{2\pi} \frac{ie^{it}}{i +e^{it} +1} dt }\)
Podstawienie:
\(\displaystyle{ i+e^{it} +1 = u, }\)
\(\displaystyle{ i e^{it} = du, }\)
\(\displaystyle{ \frac{1}{6} \int_{i+2}^{i+2} \frac{du}{u} = 0. }\)
\(\displaystyle{ \frac{1}{2} \int_{C}\frac{1}{z+1} dz = \int_{0}^{2\pi} \frac{ie^{it}}{i +e^{it} -1} dt }\)
Podstawienie:
\(\displaystyle{ I+e^{it} -1 = v, }\)
\(\displaystyle{ i e^{it} = dv, }\)
\(\displaystyle{ \frac{1}{2} \int_{i}^{i} \frac{dv}{v} = 0. }\)
\(\displaystyle{ \frac{1}{3} \int_{C}\frac{1}{z-2} = \int_{0}^{2\pi} \frac{ie^{it}}{i +e^{it} -2} dt }\)
Podstawienie:
\(\displaystyle{ i+e^{it} -2 = s, }\)
\(\displaystyle{ i e^{it} = ds, }\)
\(\displaystyle{ \frac{1}{3} \int_{i-1}^{i-1} \frac{ds}{s} = 0. }\)
Re: Całka zespolona po konturze
: 27 lis 2022, o 23:42
autor: arek1357
Wymiękam...
Re: Całka zespolona po konturze
: 28 lis 2022, o 13:51
autor: Janusz Tracz
a4karo pisze: 27 lis 2022, o 13:29
Jak znasz twierdzenie o residuach, to nic nie musisz liczyć
Masz na myśli sumę pustą? W twierdzeniu o residuach suma przebiega indeksy punktów osobliwych wewnątrz krzywej tu takowych nie ma. Więc z twierdzenia o residuach
\(\displaystyle{ \int_{C}^{} \frac{1}{(z^2-1)(z-2)} \, \dd z = 2\pi i\sum _{k\in \varnothing } \operatorname {Res} \Big( \frac{1}{(z^2-1)(z-2)} ,k-\text{ty punkt osobliwy wewnątrz }C \Big) =0. }\)
Moim zdaniem w tym zadaniu trzeba jedynie stwierdzić, że założenia twierdzenia Cauchy’ego są spełnione (to co proponuje
Dasio11). I nie mówię tu nawet o wzorze Cauchy’ego tylko o twierdzeniu podstawowym, gdzie mamy całkę z funkcji holomorficznej po krzywej zamkniętej.
@
janusz47 zwykle trzymam język za zębami i się powstrzymuje się przed komentarzami. Tyma razem jednak zrobię wyjątek ponieważ uważam, że to co napisałeś w istotny sposób (niestety negatywny) oddziałuje na osoby uczące się tego tematu. Widać, że masz jakieś pojęcie o całkach zespolonych ale pisanie czegoś takiego:
\(\displaystyle{ \int_{\Gamma} \frac{dz}{z-a} = \begin{cases} 0, \ \ a\in \Gamma \\ 2\pi i, \ \ a \notin \Gamma. \end{cases}}\)
jest po prostu wprowadzaniem w błąd. Propozycja rozkładu na ułamki proste też jest raczej dziwna. Twierdzenie Cauchy’ego można stosować bez tego rozkładu.
Re: Całka zespolona po konturze
: 28 lis 2022, o 17:53
autor: forest99
To było zadanie z egzaminu, więc - może niesłusznie założyłam, że zadanie w którym można zastosować tw. podstawowe i nic nie liczyć, byłoby zbyt proste na egzamin.
Trochę wątpliwości wprowadził też przykład z książki, gdzie jest funkcja:
\(\displaystyle{ \frac{1}{z^2+1} }\)
I ona na pierwszy rzut niedoświadczonego oka wygląda na funkcję bez biegunów, ale autor zapisuje ją jako:
\(\displaystyle{ \frac{1}{(z-i)(z+i)} }\) i okazuje się że są osobliwości w
\(\displaystyle{ i }\) oraz
\(\displaystyle{ -i}\).
Ponawiam więc pytanie z głównego posta: jak znaleźć wszystkie bieguny tego typu funkcji zespolonej?
Czy taki schemat postępowania jest poprawny:
1. Zapisuję funkcję w postaci ogólnej:
\(\displaystyle{ z^3 - 2z^2 - z + 2}\)
2. Wielomian jest stopnia 3, więc jeśli znalazłam już 3 pierwiastki:
\(\displaystyle{ z_{0} =1}\),
\(\displaystyle{ z_{0}=-1}\) i
\(\displaystyle{ z_{0}=2}\), to mam już pewność, że to wszystkie bieguny
3. Jeśli nie, to stosuję algorytmy pierwiastkowe dla wielomianu 3 stopnia - algorytm Ferro?
https://edu.pjwstk.edu.pl/wyklady/alg/scb/index26.html