To świetnie. Czy w takim razie ze szczegółami rozwiązania już sobie dasz radę na podstawie tego co napisałem?
Dodano po 1 dniu 3 godzinach 48 minutach 11 sekundach:
W międzyczasie też już sobie poradziłem z tą równością:
\(\sin\frac{4\pi}{30}\;\sin\frac{8\pi}{30}=\sin\frac{3\pi}{30}\;\sin\frac{13\pi}{30}\).
Podaję główne kroki, gdyby ktoś chciał to prześledzić. Iloczyn sinusów zamieniamy na różnicę kosinusów, równanie mnożymy przez \(2\). Argumenty zapisujemy używając ułamków \(\frac{\pi}{5}\) i \(\frac{\pi}3\).
\(\cos\left(\frac{\pi}5-\frac{\pi}3\right) - \cos\frac{2\pi}5= \cos\frac{\pi}3 - \cos\left(\frac{\pi}5+\frac{\pi}3\right)\)
Po skorzystaniu ze wzoru na kosinus różnicy/sumy i uproszczeniach mamy:
\(2\cos\frac{\pi}5\;\cos\frac{\pi}3 = \cos\frac{2\pi}5 + \cos\frac{\pi}3\).
Dalej wystarczy już tylko podstawić wartości i zobaczyć, że się zgadza:
\(2\cdot\frac{\sqrt5+1}4\cdot\frac12=\frac{\sqrt5-1}4+\frac12\).
W tym zadaniu znalazłem ciekawostkę. W programie takim jak Geogebra można zaobserwować, co się stanie gdy zmienimy wartości kątów \(18^{\circ}\) i \(24^{\circ}\) na inne. Chciałem w ten sposób zobaczyć, kiedy punkty \(E'\) i \(A\) leżą symetrycznie względem prostej \(CE\). Na podstawie moich obserwacji wysnułem hipotezę, że istotna tu jest rozwartość kąta równa \(18^{\circ}\). Gdy zmieniałem tylko drugi kąt (\(\sphericalangle BDE\)), punkty \(E'\) i \(A\) zdawały się leżeć symetrycznie względem dwusiecznej. Zatem, czy zadanie ma również ładny wynik dla kąta \(\sphericalangle CED = 18^{\circ}\) i kąta \(\sphericalangle BDE\) zmieniającego się w pewnym zakresie?
Przy założeniu prawdziwości hipotezy, mielibyśmy trygonometryczną tożsamość ogólniejszą niż poprzednio:
\(\sin x\cdot \sin\left(\frac{2\pi}5-x\right)=\sin\frac{\pi}{10}\cdot \sin\left(4x - \frac{\pi}{10}\right)\),
gdzie \(x\) oznacza miarę kąta \(\sphericalangle BDE\). Równość jest spełniona dla \(x=\frac{2\pi}{15}=24^{\circ}\) (co wykazaliśmy wyżej) i dla \(x=\frac{\pi}{10}=18^{\circ}\) (co odpowiada trójkątowi równoramiennemu), jednak nie jest spełniona dla \(x=0\). Warto spojrzeć na wykresy lewej i prawej strony (na przykład w Wolframie), żeby zobaczyć, o co chodzi.
Kod: Zaznacz cały
https://www.wolframalpha.com/input?i=sin%28x%29+*+sin%2812*pi%2F30-x%29+%3D+sin%283*pi%2F30%29+*+sin%284*x-3*pi%2F30%29
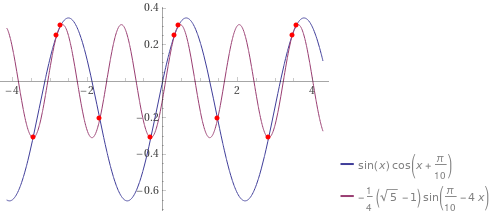
- MSP17961458h81ce0i5gf4e00002ab67c5g2f4151f6.gif (10.91 KiB) Przejrzano 621 razy
W przedziale od \(\frac{\pi}{10}\) do \(\frac{2\pi}{15}\) funkcje niewiele się różnią, co jednak nie znaczy że są takie same.
Morał jest taki, że nawet jeśli na rysunku coś widać, to warto to poprzeć dowodem.