Strona 1 z 2
Narysować podany sygnał oraz wyznaczyć jego poziom
: 8 kwie 2020, o 22:45
autor: pomiatacz
Dzień dobry mam problem z zadaniem, gdzie sygnał prostokątny o różnej amplitudzie mam pomnożyć przez sinus. Jak narysować to na jednym wykresie oraz co oznacza polecenie wyznaczenia poziomu sygnału dla chwili = 1,5s.
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 8 kwie 2020, o 23:12
autor: janusz47
1. Zapisujemy sygnał wejściowy - prostokątny \(\displaystyle{ r(t) }\) wzorem "klamerkowym".
2. Obliczamy transformatę tego sygnału \(\displaystyle{ R(s). }\)
3. Wyznaczamy transformatę sygnału sinusoidalnego \(\displaystyle{ S(s). }\)
4. Obliczamy splot sygnałów \(\displaystyle{ Y(s) = R(s)* S(s). }\)
5. Wyznaczamy odwrotną transformatę splotu (oryginał)
\(\displaystyle{ y(t) = L^{-1}[Y(s)]. }\)
Obliczamy wartość poziomu sygmału \(\displaystyle{ y(1,5). }\)
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 9 kwie 2020, o 07:31
autor: kerajs
Hmm... , po co w tak łatwym przykładzie przechodzić na zapis operatorowy, skoro :
\(\displaystyle{ r(t)=1{\hskip -2.5 pt}\hbox{l}(t)- \frac{3}{2} 1{\hskip -2.5 pt}\hbox{l}(t-1)+ \frac{5}{2} 1{\hskip -2.5 pt}\hbox{l}(t-2)-3 1{\hskip -2.5 pt}\hbox{l}(t-2,5)+ 1{\hskip -2.5 pt}\hbox{l}(t-3)}\)
a iloczyn
\(\displaystyle{ y(t)=r(t)s(t)=(1{\hskip -2.5 pt}\hbox{l}(t)- \frac{3}{1} 1{\hskip -2.5 pt}\hbox{l}(t-1)+ \frac{5}{2} 1{\hskip -2.5 pt}\hbox{l}(t-2)-3 1{\hskip -2.5 pt}\hbox{l}(t-2,5)+ 1{\hskip -2.5 pt}\hbox{l}(t-3))\sin 2 \pi t }\)
A w praktyce, to rysuje się sinusoidę (ma ona okres 1) i odpowiednio zmienia jej amplitudę.
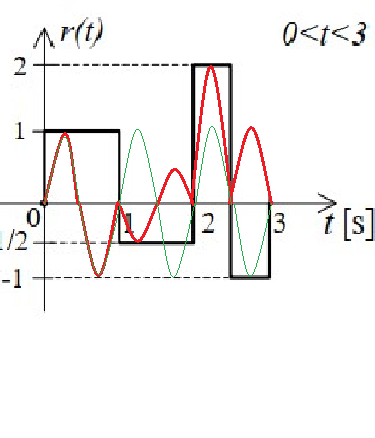
- wzl2.png (31.41 KiB) Przejrzano 5810 razy
Wartość czerwonego sygnału dla t=1,5 s dość łatwo odczytać z wykresu.
PS
A skąd wiadomo że
\(\displaystyle{ y(t)=r(t)s(t)}\) , a nie
\(\displaystyle{ y(t)=r(t)+s(t)}\) ?
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 9 kwie 2020, o 09:00
autor: janusz47
W teorii sygnałów, aby porządnie rozwiązać to zadanie przechodzi się na transformaty ioryginał. Znak kółeczka z X wskazuje, że mamy do czynienia ze splotem.
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 9 kwie 2020, o 14:05
autor: a4karo
A w teorii całki żeby porządnie obliczyć objętość sześcianu, trzeba napisać całkę potrójną

Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 9 kwie 2020, o 19:04
autor: pomiatacz
kerajs pisze: 9 kwie 2020, o 07:31
Hmm... , po co w tak łatwym przykładzie przechodzić na zapis operatorowy, skoro :
\(\displaystyle{ r(t)=1{\hskip -2.5 pt}\hbox{l}(t)- \frac{3}{2} 1{\hskip -2.5 pt}\hbox{l}(t-1)+ \frac{5}{2} 1{\hskip -2.5 pt}\hbox{l}(t-2)-3 1{\hskip -2.5 pt}\hbox{l}(t-2,5)+ 1{\hskip -2.5 pt}\hbox{l}(t-3)}\)
a iloczyn
\(\displaystyle{ y(t)=r(t)s(t)=(1{\hskip -2.5 pt}\hbox{l}(t)- \frac{3}{1} 1{\hskip -2.5 pt}\hbox{l}(t-1)+ \frac{5}{2} 1{\hskip -2.5 pt}\hbox{l}(t-2)-3 1{\hskip -2.5 pt}\hbox{l}(t-2,5)+ 1{\hskip -2.5 pt}\hbox{l}(t-3))\sin 2 \pi t }\)
A w praktyce, to rysuje się sinusoidę (ma ona okres 1) i odpowiednio zmienia jej amplitudę.
wzl2.png
Wartość czerwonego sygnału dla t=1,5 s dość łatwo odczytać z wykresu.
PS
A skąd wiadomo że
\(\displaystyle{ y(t)=r(t)s(t)}\) , a nie
\(\displaystyle{ y(t)=r(t)+s(t)}\) ?
Tylko ja potrzebuje wyznaczyć poziom sygnału dla danej chwili, a nie jego wartość. Z tego co wyczytałem to jest to miara logarytmiczna
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 9 kwie 2020, o 20:14
autor: kerajs
1. Przypominam, że zadałem dość istotne pytanie:
kerajs pisze: 9 kwie 2020, o 07:31
A skąd wiadomo że
\(\displaystyle{ y(t)=r(t)s(t)}\) , a nie
\(\displaystyle{ y(t)=r(t)+s(t)}\) ?
2. Przypominam, że
janusz47 podważył poprawność mojego rozwiązania. Wie z jakiego przedmiotu jest to zadanie i jaka jest tam metodologia rozwiązywania zadań. Możesz się do tego ustosunkować?
3. Przypominam, że nie podałeś żadnej definicji. Równie dobrze poziomem sygnału może być bezwzględny stosunek sygnału wyjściowego do wejściowego lub bazowego (na którym modulowany jest inny sygnał), czyli odczytane z rysunku
\(\displaystyle{ \left| \frac{0}{-0,5} \right|=0}\)
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 9 kwie 2020, o 22:10
autor: janusz47
Teoria sygnałów
\(\displaystyle{ \mathcal{L}[r(t)] = R(s) = \frac{1}{s^2} - \frac{3s-1}{2s^2} + \frac{5 -10s}{2s^2} - \frac{3 -7,5s}{s^2}+ \frac{1-3s}{s^2} = \frac{4 - 4s}{2s^2} = \frac{2-2s }{s^2}}\)
\(\displaystyle{ \mathcal{L} [s(t)] = S(s) = \mathcal{L}[\sin(2\pi\cdot t)] = \frac{2\pi}{s^2 +4\pi^2}. }\)
\(\displaystyle{ Y(s) = R(s)*S(s) = \frac{2 -2s}{s^2}\cdot \frac{2\pi}{s^2 +4\pi^2} = \frac{2\pi( 2-2s)}{ s^4 +(2\pi s)^2} = \frac{4\pi(1-s)}{s^4 +(2\pi s)^2}. }\)
\(\displaystyle{ y(t) = \mathcal{L}^{-1}[Y(s)] = \mathcal{L}^{-1}\left [ \frac{4\pi( 1- s)}{ s^4 +(2\pi s)^2} \right] = \frac{2\pi \cdot t - \sin(2\pi \cdot t)+ 2\pi[\cos(2\pi\cdot t)-1]}{ 2\pi^2}. }\)
Poziom sygnału dla \(\displaystyle{ t = 1,5 s }\)
\(\displaystyle{ y(1,5) = \frac{2\cdot 1,5\pi -\sin(3\pi) + 2\pi[\cos(3\pi) -1]}{2\pi^2} = \frac{ 3\pi - 0 +2\pi -2\pi)}{4\pi^2}= \frac{3\pi}{2\pi^2} = \frac{3}{2\pi}.}\)
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 10 kwie 2020, o 04:44
autor: a4karo
janusz47 pisze: 9 kwie 2020, o 22:10
Teoria sygnałów
\(\displaystyle{ \mathcal{L}[r(t)] = R(s) = \frac{1}{s^2} - \frac{3s-1}{2s^2} + \frac{5 -10s}{2s^2} - \frac{3 -7,5s}{s^2}+ \frac{1-3s}{s^2} = \frac{4 - 4s}{2s^2} = \frac{2-2s }{s^2}}\)
\(\displaystyle{ \mathcal{L} [s(t)] = S(s) = \mathcal{L}[\sin(2\pi\cdot t)] = \frac{2\pi}{s^2 +4\pi^2}. }\)
\(\displaystyle{ Y(s) = R(s)*S(s) = \frac{2 -2s}{s^2}\cdot \frac{2\pi}{s^2 +4\pi^2} = \frac{2\pi( 2-2s)}{ s^4 +(2\pi s)^2} = \frac{4\pi(1-s)}{s^4 +(2\pi s)^2}. }\)
Chcesz powiedzieć, że \(*=\cdot\) ???
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 10 kwie 2020, o 11:58
autor: janusz47
Chciałem powiedzieć, że znak splotu w schemacie, odpowiada zwykłemu mnożeniu transformat.
\(\displaystyle{ Y(s) =\mathcal{L}[ r(t)* s(t)] = R(s)\cdot S(s) }\)
Korekta:
\(\displaystyle{ y(1,5) = \frac{2\cdot 1,5\pi -\sin(3\pi) + 2\pi[\cos(3\pi) -1]}{2\pi^2} = \frac{ 3\pi - 0 -2\pi -2\pi)}{4\pi^2}= -\frac{\pi}{2\pi^2} = -\frac{1}{2\pi}.}\)
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 10 kwie 2020, o 13:17
autor: a4karo
Niby tak, ale masz do policzenia \(\mathcal{L}[r(t)s(t)]\) a nie \(\mathcal{L}[r(t)*s(t)]\)
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 10 kwie 2020, o 14:42
autor: kerajs
janusz47 pisze: 9 kwie 2020, o 22:10
Teoria sygnałów
\(\displaystyle{ \mathcal{L}[r(t)] = R(s) = \frac{1}{s^2} - \frac{3s-1}{2s^2} + \frac{5 -10s}{2s^2} - \frac{3 -7,5s}{s^2}+ \frac{1-3s}{s^2} = (...)}\)
Pozwolę sobie pokazać transformatę odwrotną powyższego R(s)
\(\displaystyle{ r(t)=L^{-1}\left\{ R(s)\right\}=t- \frac{3}{2}1{\hskip -2.5 pt}\hbox{l}(t)+ \frac{1}{2}t + \frac{5}{2}t- \frac{10}{2}1{\hskip -2.5 pt}\hbox{l}(t)-3t +7,5 1{\hskip -2.5 pt}\hbox{l}(t)+ t-\frac{3}{2}1{\hskip -2.5 pt}\hbox{l}(t) =2t-\frac{1}{2}1{\hskip -2.5 pt}\hbox{l}(t)}\)
Moim zdaniem nie jest to sygnał z rysunku.
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 10 kwie 2020, o 14:51
autor: janusz47
Nie patrzyłem na rysunek, wzorowałem się na zapisie \(\displaystyle{ r(t) }\) po "Hmm"
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 10 kwie 2020, o 16:10
autor: kerajs
O, czyżbyś mój opis r(t) uznał za poprawny. Wow!
Szkoda tylko, że tak zsoliłeś jego transformatę.
Skoro nie znasz lub źle pamiętasz transformaty ze skoku jednostkowego to je przypomnę:
\(\displaystyle{ L(1{\hskip -2.5 pt}\hbox{l}(t))= \frac{1}{s}\\
L(1{\hskip -2.5 pt}\hbox{l}(t-t_0))= \frac{e^{-t_0s}}{s} \ \ \text{dla} \ \ t_0>0 }\)
Zastosuj je, a może tym razem uzyskasz poprawny wynik.
PS
\(\displaystyle{ \int_{0}^{ \infty } f(t) e^{-st} dt= \int_{0}^{ \infty } 1{\hskip -2.5 pt}\hbox{l}(t-t_0)e^{-st} dt= \int_{0}^{t_0 } 0 \cdot e^{-st} dt+ \int_{t_0}^{ \infty } 1 \cdot e^{-st} dt=\\=
\int_{0}^{t_0 } 0 dt+ \int_{t_0}^{ \infty } e^{-st} dt=0+ \frac{-e^{-st}}{s}\bigg|_{t_0}^{ \infty } = \frac{-e^{- \infty }}{s}-\frac{-e^{-st_0}}{s}=0+\frac{e^{-t_0s}}{s}=\frac{e^{-t_0s}}{s}}\)
Re: Narysować podany sygnał oraz wyznaczyć jego poziom
: 10 kwie 2020, o 16:30
autor: janusz47
Proszę poprawić i nie krytykować. Mógłby też krytykować nie tylko teorię, ale i rysunek. Staram się opanowywać własne Wow!