Strona 1 z 1
Kawiarnia Jaś i Małgosia.
: 29 cze 2019, o 23:57
autor: Piasek96
Jaś umówił się z Małgosią w kawiarni. Oboje zdecydowali się w razie potrzeby czekać nawzajem na siebie, ale nie dłużej niż kwadrans. Zakładając że oboje przychodzą do kawiarni w losowo wybranym momencie pomiędzy 16:00 a 17:00, oblicz prawdopodobieństwo,że ich spotkanie dojdzie do skutku.
Re: Kawiarnia Jaś i Małgosia.
: 30 cze 2019, o 00:31
autor: kerajs
Niech
\(\displaystyle{ x}\) oznacza moment dotarcia na miejsce spotkania pierwszej osoby, a
\(\displaystyle{ y}\) czas przyjścia drugiej osoby.
Wszystkie możliwe terminy reprezentuje obszar tych punktów
\(\displaystyle{ (x,y)}\) gdzie
\(\displaystyle{ x, y \in \left\langle 16,17\right\rangle}\)

- 1.jpg (25.74 KiB) Przejrzano 99 razy
Pole tego obszaru to 1.
Osoby się spotkają gdy różnica miedzy czasami ich przyjścia na umówione miejsce nie przekracza 15 minut, czyli 1/4 godziny. Stad:
\(\displaystyle{ \left| y-x\right| \le \frac{1}{4} \\
\frac{-1}{4} \le y-x \le \frac{1}{4} \\
x+ \frac{-1}{4} \le y \le x + \frac{1}{4}}\)
Zaznaczam ten obszar na rysunku:
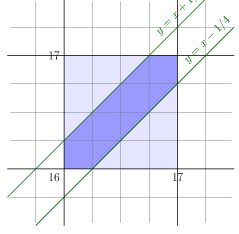
- 2.jpg (38.89 KiB) Przejrzano 99 razy
Pole tego obszaru to:
\(\displaystyle{ 1-2 \cdot \left[ \frac{1}{2} \cdot \frac{3}{4} \cdot \frac{3}{4} \right]= \frac{7}{16}}\)
Szukane prawdopodobieństwo to stosunek pól:
\(\displaystyle{ P= \frac{\frac{7}{16}}{1} =\frac{7}{16}}\)