Nie wiem czy nie powinniśmy się przenieść z tym do "Twojego" tematu
Fermion pisze:Czy mógłbyś jakoś na szybko opisać jak rozumieć "podejście perturbacyjne" i "nieperturbacyjne". Nie widzę żadnego fajnego opisu a trudno mi zrozumieć całość Twojego postu bez tego.
1. Nie wiem czy spotkałeś się kiedyś z czymś takim jak rozwijanie funkcji w szereg:
Kod: Zaznacz cały
https://pl.wikipedia.org/wiki/Szereg_Taylora
. Mniej więcej chodzi o to, że przedstawiamy funkcję jako "nieskończoną sumę" prostszych składników. W ten sposób oblicza się np. wartości funkcji trygonometrycznych.
2. Metody perturbacyjne polegają na tym, że rozwijamy w szereg rzeczy które albo ciężko obliczyć, albo wręcz nie da się ich ręcznie obliczyć. Robi się to w całej fizyce, np. w elektrodynamice znane jest rozwinięcie multipolowe przy okazji którego pojawiają się takie znane nazwy jak dipol czy kwadrupol.
Doświadczalna weryfikacja kwantowej teorii pola polega zwykle na zderzaniu cząstek i patrzeniu co z tego wyjdzie. Powiedzmy, że chcemy obliczyć prawdopodobieństwo tego, że z elektronu i pozytonu na wejściu dostaniemy to samo na wyjściu, czyli prawdopodobieństwo takiej reakcji
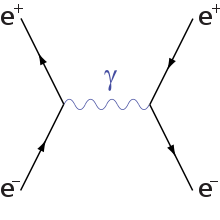
\(\displaystyle{ e^-+e^+\rightarrow e^-+ e^+}\). Dostajemy pewne wyrażenie, którego nie da się obliczyć ręcznie. Zapisujemy je zatem jako sumę (nieskończoną) małych kawałków, które jesteśmy w stanie obliczyć analitycznie. Tylko wciąż są to wyrażenia bardzo skomplikowane. Całe szczęście Feynman zauważył, że to co dostajemy po wstępnych przekształceniach, które właściwie są najtrudniejszą częścią tej zabawy, można przedstawić rysunkowo. Rysunki te nazywamy diagramami Feynmana. I w praktyce to wygląda tak, że pomijamy te wstępne przekształcenia i od razu rysujemy odpowiednie diagramy, stosując się do odpowiednich reguł, zwanych regułami Feynmana. Każdemu elementowi tego rysunku coś odpowiada. Tu masz przykładowy diagram (jeden z dwóch) drugiego rzędu dla wspomnianej przeze mnie reakcji:
- AU
- 220px-Bhabha_S_channelsvg.png (4.84 KiB) Przejrzano 2008 razy
Ten diagram nie obrazuje w żadnym wypadku tego jak to "wygląda" w rzeczywistości, on opisuje tylko i wyłącznie matematykę. Wierzchołkom zewnętrznym odpowiadają odpowiednie spinory, potem liniom elektronu i pozytonu ich propagatory, a linia wewnętrzna, zwana w tym przypadku
wirtualnym fotonem, reprezentuje wyrażenie matematyczne zwane propagatorem fotonu, który wygląda tak:
\(\displaystyle{ \frac{-ig_{\mu \nu}}{p^2+i\varepsilon}}\). Oto wirtualny foton w całej okazałości
Ale chodzi przede wszystkim o to, że jeśli nie używamy metod perturbacyjnych, to nie ma cząstek wirtualnych, bo nie ma diagramów Feynmana. A nie wszędzie się da ich używać. Np. w chromodynamice kwantowej oddziaływania są za silne, żeby szereg perturbacyjny dawał sensowne wyniki. Albo rozpatrując kwantowe teorie pola w mniejszej liczbie wymiarów, np.
\(\displaystyle{ 1+1}\), czy
\(\displaystyle{ 1+2}\) dostajemy wyrażenia, które jesteśmy w stanie obliczyć bez uciekania się do takich metod. I wtedy żadne cząstki wirtualne się nie pojawiają. To jest tylko efekt uboczny naszych metod matematycznych i widać to bardzo dobrze jak się człowiek zagłębi w formalną strukturę perturbacyjnej kwantowej teorii pola. Jej ścisłe geometryczne sformułowanie istnieje już od dość dawna, ale jest znane głównie fizykom matematycznym. Większość fizyków nic o tym nie wie, bo w gruncie rzeczy nie jest im to do niczego potrzebne
Angielskojęzyczne opisy na youtube różnych osób sugerowały to co napisałem i zgadzało się to z opisem wikipedii. Dlatego myślałem że widocznie te cząstki są realne skoro wywierają ciśnienie.
Żeby było śmiesznie, to pierwsze słyszę o ciśnieniu wywieranym przez cząstki wirtualne. Ale nie jest to oczywiście poprawne wyjaśnienie, nawet jeśli używać opisu perturbacyjnego. Wyrażenia matematyczne nie mogą wywierać ciśnienia
Żeby tak nie być gołosłownym, to opiszę standardowe zadanie z elektrodynamiki kwantowej, w którym pojawia się zagadnienie efektu Casimira. Załóżmy, że mamy dwie kwadratowe płyty o boku
\(\displaystyle{ L}\), oddalone od siebie od
\(\displaystyle{ a}\) i problem polega na opisaniu pola elektromagnetycznego pomiędzy tymi płytami. Zakładamy, że są one idealnymi przewodnikami. Najpierw rozwiązujemy klasyczne równanie Maxwella dla potencjału elektromagnetycznego
\(\displaystyle{ \vec{A}}\) w takim układzie. Wynik jest dany w postaci szeregu. Następnie przeprowadzamy standardową kanoniczną kwantyzację otrzymanego wyniku, awansując współczynniki pojawiające się w tym szeregu do operatorów spełniających odpowiednie relacje komutacyjne. Wykorzystujemy te relacje do wyznaczenia hamiltonianu
\(\displaystyle{ H}\) układu. Mając hamiltonian możemy przejść do najciekawszej rzeczy, czyli obliczenia wartości energii pola elektromagnetycznego między płytami. Energia ta jest dana wzorem:
\(\displaystyle{ \langle 0|H|0 \rangle =\frac{L^2}{2 \left( 2\pi \right) ^2}\int\textsf{d}^2k \left( 2\sum_{n=1}^\infty \sqrt{k_1^2+k_2^2+ \left( \frac{n\pi}{a} \right) ^2}+\sqrt{k_1^2+k_2^2} \right)}\)
gdzie
\(\displaystyle{ k_1, k_2}\) to stałe, które pojawiły się we wcześniejszych wyprowadzeniach. Całkujemy po pędach pola. Interesuje nas jaka jest różnica między tą energią, a energią pola przy braku płyt:
\(\displaystyle{ \langle 0|H_0|0 \rangle=\int\frac{L^2\textsf{d}^2k}{(2\pi)^2}\int_{\mathbb{\RR_+}}\textsf{d}n\sqrt{k_1^2+k_2^2+ \left( \frac{n\pi}{a} \right) ^2}}\).
Okazuje się, że różnica tych energii przypadająca na jednostkę powierzchni płyt jest dana wzorem (po usunięciu kilku nieskończoności ):
\(\displaystyle{ \epsilon=-\frac{\pi^2}{720a^3}}\)
Siła Casimira przypadająca na jednostkę powierzchni jest dana wzorem:
\(\displaystyle{ f=-\frac{\partial\epsilon}{\partial a}=-\frac{\pi^2}{240a^4}}\)
I gotowe. Bez cząstek wirtualnych
Wiem, że wikipedia nie jest wyrocznią ale nie można powiedzieć ze są tam same bzdury bo wg mnie w znacznej większości przypadków jest to ściśle i porządnie opisane.
W znacznej większości prostych przypadków owszem, ale efekt Casimira do prostych nie należy.
Chyba że możesz opisać to na zasadzie : elektrony w płytach mają ładunki, oddziałują one z polem drugiej płyty, i w wyniku tego to i tamto (oczywiście to nie ma sensu co napisałem ale taki opis wydawałby mi się przystępniejszy jakbyś mógł).
Ma to jak najbardziej sens. Oddziaływanie zbioru związanych ładunków z jednej płyty ze zbiorem związanych ładunków drugiej płyty. Ich obecność powoduje istnienie fluktuacji energii pola między płytami, która to fluktuacja prowadzi do istnienia siły Casimira. Cóż więcej chcieć Wiem, że człowiek lubi takie mechanistyczne wyjaśnienia typu "cząstki uderzają płyty i je popychają", ale takiego wyjaśnienia nie ma i trzeba się z tym trochę pogodzić.
Teraz to ja nawet nie mam możliwości dyskusji z nikim na ten temat. Bo jak powiem że to nie cząstki wirtualne to mnie zarzucą materiałami że to cząstki wirtualne
Ale jakimi materiałami? Wikipedią? YouTubem? Zawsze możesz im wysłać linki do różnych publikacji, jak np. tej: . Niech z tym dyskutują. Albo z podręcznikami, np.
Student Friendly Quantum Field Theory Roberta Klaubera. Strona 271
dlaczego sama wikipedia pisze że to cząstki wirtualne wywierają ciśnienie. Nawet grafika na wikipedii to sugeruje.
Z tą wikipedią to tak śmiesznie jest. Znam kilku fizyków, profesorów, specjalistów w dziedzinie kosmologii czy właśnie kwantowej teorii pola, którzy próbowali poprawiać artykuły na angielskiej wikipedii. Wszystkie ich poprawki były zawsze cofnięte. Wikipedia jest spoko do tematów łatwych, tematy specjalistyczne nie zawsze są dobrze opisane.
Rozumiem ze Hawking tak to tłumaczył, nie był z tego zadowolony i po latach znaleziono inny opis.
Nie nie nie. Hawking tak to tłumaczył
w książkach popularnonaukowych. I z tego był niezadowolony, że nie był w stanie tego wyjaśnić laikom w lepszy sposób. Jego ścisły oryginalny opis pozostaje cały czas w mocy, tylko nie ma tam
w ogóle wirtualnych cudów. Tzn. wspomina o cząstkach wirtualnych w ramach heurystycznego wstępnego opisu, ale dalej ich nie używa. Co więcej, o ile mi wiadomo to nikt do tej pory nie wyprowadził promieniowania Hawkinga w taki lokalny, perturbacyjny sposób, w którym to pojawiłyby się cząstki wirtualne.
interesuje mnie jak to tłumaczą Profesorowie fizyki na studiach (lub Twoje zdanie jeśli masz odmienne)
Moje zdanie w ugruntowanych sprawach jest zawsze zgodne z oficjalną wykładnią Swoje zdanie mam tam, gdzie faktycznie można mieć jakieś zdanie. Promieniowania Hawkinga nie zaobserwowano, bo nie ma w tej chwili takiej możliwości. Jest ono po prostu za słabe. A wyprowadza się je w obrębie kwantowej teorii pola w zakrzywionych czasoprzestrzeniach i przetłumaczenie tego na zwykły język jest dużo trudniejsze niż w przypadku efektu Casimira. Szczerze mówiąc to nawet nie bardzo wiem jak to zrobić. Wszystko się opiera na tym, że przejście z płaskiej czasoprzestrzeni Minkowskiego do czasoprzestrzeni zakrzywionej zmienia bardzo dużo w opisie, bo takie pojęcia jak próżnia czy cząstka (która już w zwykłej płaskiej czasoprzestrzeni jest pojęciem nie zawsze definiowalnym) są względne. Dwóch różnych obserwatorów może mieć inne zdanie co do tego co to stan próżni, albo czy jest obecna cząstka czy antycząstka. Oczywiście te ich zdania są ze sobą matematycznie związane, to nie jest tak że wszystko się tu może zdarzyć. To matematyczne powiązanie nazywa się transformacją Bogoliubova. Obiektywna, obserwowana przez wszystkich kreacja par cząstka-antycząstka nie ma z promieniowaniem Hawkinga żadnego związku. Blisko horyzontu zdarzeń pole rozszczepia się na dwie części: o dodatniej i ujemnej energii (względem odpowiedniego punktu odniesienia). Jest to efekt oddziaływania z "polem grawitacyjnym" czarnej dziury. To o ujemnej zostaje za horyzontem, a to o dodatniej pozostaje poza horyzontem. W tym procesie obiektywnie obserwuje się przepływ energii i pędu z czarnej dziury, przez co jej masa maleje, ale nie każdy obserwator zobaczy cząstki. Ten który jest blisko horyzontu zdarzeń może zobaczyć kreację pary cząstka-antycząstka, ale nie przez cząstki wirtualne, tylko przez silne pole grawitacyjne czarnej dziury. Stąd utrata energii przez czarną dziurę, bo pole wytwarza te cząstki kosztem własnej energii. Podobny efekt kreacji zachodzić może w silnym polu elektromagnetycznym, tylko nie został jeszcze nigdy zaobserwowany, bo pola wytwarzane na Ziemi są za słabe. Nazywa się to efekt Schwingera.
Czy słuszne jest stwierdzenie że jeśli czarne dziury mają tą samą masę, ładunek i moment pędu to są nieodróżnialne ?
Tak.
i to ten moment wyobrazili sobie jako wielki wybuch bo od razu widać ze coś dziwnego wtedy się dzieje. Ponadto wraz ze zbliżaniem się do chwili wielkiego wybuchu odległość pomiędzy dowolnymi dwiema cząstkami materii maleje do zera. Z tego powodu można sobie wyobrażać, że w chwili wielkiego wybuchu wszechświat był „skurczony do rozmiarów punktu”
Termin "wielki wybuch" odnosi się bardziej do samego procesu gwałtownego rozszerzania się czasoprzestrzeni niż do osobliwości. Z tym skurczeniem do rozmiarów punkt, to działa to tylko jeśli założyć, że Wszechświat ma skończony rozmiar. Jeśli jest nieskończony, a tak sądzimy na podstawie zerowej krzywizny przestrzennej, to był nieskończony zawsze.
Więc wielki wybuch jest "tworem intuicji" fizyków badających modele kosmologiczne ale nie mamy żadnych dowodów ze faktycznie miał miejsce.
Jak pisałem wyżej, w standardowym modelu kosmologicznym
\(\displaystyle{ \Lambda}\)-CDM "wielki wybuch" odnosi się do samego procesu, a nie do osobliwości. A zajścia tego procesu jesteśmy praktycznie pewni, gdyż teoria Wielkiego Wybuchu w takiej formie w jakiej faktycznie istnieje, a nie w formie w jakiej jest kreowana przez popularyzatorów, ma
ogromne poparcie obserwacyjne i doświadczalne. Osobliwości nikt nie traktuje jako fizycznej i realnej, gdyż jak wykazali Hawking i Penrose, praktycznie każde sensowne rozwiązanie równań Einsteina ma osobliwość. To świadczy o tym, że OTW jest teorią niekompletną, a nie o tym, że gdzieś kiedyś gęstość i krzywizna były nieskończone
Czy dekoherencja to też przeżytek?
Nie nie, dekoherencja jest wciąż żywa.
PS. Za wszelkie powtórzenia i nieskładne zdania przepraszam. Od 4 dni mam korki od rana do wieczora i już mi mózg przestaje dobrze funkcjonować