Strona 1 z 1
Reakcje w układzie prętów
: 24 lis 2018, o 15:13
autor: kasia_lovatic
Mam problem z rozkładem sił F gdyż jest ona pod katem prostem, jakas wskazowka?
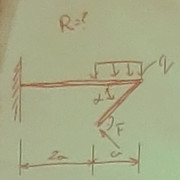
- AU
- aaaaaaaa.jpg (6.16 KiB) Przejrzano 398 razy
[/url]
Re: Reakcje w układzie prętów
: 24 lis 2018, o 15:39
autor: kruszewski
Za biegun redukcji wziąć nieutwierdzony koniec belki (poziomej) i zredukować działanie na nią siły \(\displaystyle{ \vec{F}}\) do wektora \(\displaystyle{ \vec{F}}\) i momentu \(\displaystyle{ M_r = F \cdot \frac{a}{\cos \alpha }}\) i rozwiązywać belkę obciążoną : obciążeniem ciągłym \(\displaystyle{ q}\) , siłą \(\displaystyle{ \vec{F}}\) i momentem skupionym \(\displaystyle{ M_r}\), zaś ukośne ramię prostopadłą do niego siłą \(\displaystyle{ \vec{F}}\)-- 25 lis 2018, o 03:17 --
kolejno odgóry:
fig.1 wg treści zadania;
fig. 2 obciążenie belki poziomej głównymi, wektorem i momentem po zredukowaniu ich do biegona
fig. 3 obciążenie beleczki ukośnej, którą traktuje się jako utwierdzoną w belce poziomej.
Re: Reakcje w układzie prętów
: 26 lis 2018, o 22:02
autor: siwymech
Propozycja rozw.
1. Zastępujemy obciążenie ciągłe pręta siła skupioną- \(\displaystyle{ Q=q \cdot a}\)
2.Uwalniamy pręty od więzów:
-w punkcie A od utwierdzenia(dwie składowe reakcji i moment utwierdzenia),
- w przegubie B -dwie składowe reakcji
3. Analizujemy układ sił
Mamy rozwiązać układ sił dowolny płaski- złożony, statycznie niewyznaczalny, stąd przekształcamy go na dwa układy proste statycznie wyznaczalne rozłączając pręty w przegubie -punkcie B, przykładając w nim stosowne reakcje.
4. Dla każdego układu z osobna wypisujemy warunki równowagi. Rozpoczynamy od układu najprostszego- układu 2.
Re: Reakcje w układzie prętów
: 26 lis 2018, o 22:54
autor: kruszewski
W czym tu leży hiperstatyczność ?
W \(\displaystyle{ B}\) nie ma przegubu, jest to zatem załamana sztywna belka.
Zatem siła \(\displaystyle{ F}\) skutkuje w \(\displaystyle{ B}\) nie tylko składowymi \(\displaystyle{ F_x \ i \ F_y}\) jako reakcjami ale i momentem skupionym \(\displaystyle{ M_B^{(F)} = \vec{F} \cdot |AB|}\)-- 29 lis 2018, o 12:30 --
Niech nieważka ale sztywna belka ukośna dugości \(\displaystyle{ AO=r}\) połączona będzie z belką poziomą beztarciowym przegubem w \(\displaystyle{ O}\) .
Przyłożona dowolna siła \(\displaystyle{ P}\) ma kierunek prostopadły do osi podłużnej belki (jak w zadniu).
Pytamy o reakcje w sugerowanym przegubie \(\displaystyle{ O}\) belki poziomej.
Równania równowagi:
\(\displaystyle{ R_x - P_x =0 [ ex] .....(1)
\(\displaystyle{ R_y + P_y = 0}\) ......(2)
\(\displaystyle{ M_o -M_{u=r} = 0}\) .......(3)
Równość (3) napiszemy tak:
\(\displaystyle{ M_o - P \cdot r =0}\) .......(4)
Ale z definicji beztarciowego przegubu \(\displaystyle{ M_o =0}\) ......(5)
Zatem \(\displaystyle{ P \cdot r =0}\) ......(6)
W równości tej \(\displaystyle{ r >0}\) ,
zatem warunkiem spełnienia (6) jest
\(\displaystyle{ P=0}\) ...... (7)
Stąd należy wyprowadzić wniosek, że do belki, jednostronnie podpartej przegubem beztarciowym
nie można przyłożyć dowolnej siły nie leżącej w osi podłużnej belki bez naruszenia niezmienności geometrycznej ustroju.
Zatem w zadaniu tym belki są w narożu sztywno ze sobą połączone .}\)