Strona 1 z 1
Znalezienie miary kąta w okręgu
: 22 wrz 2018, o 23:24
autor: kieubass
Mam problem, uczennica na korepetycjach zapodała mi takie zadanko, gdzie trzeba obliczyć miarę kąta zaznaczonego na czerwono. Skorzystałem z twierdzenia o czworokącie wpisanym w okrąg, wszystko ładnie pięknie, tylko... Uczennica (2 klasa LO, poziom rozszerzony) nie miała jeszcze tego twierdzenia, będzie je miała za jakieś 2-3 miesiące
Czy ktoś z Was widzi jakiś inny sposób na to? Bo ja to z geometrii zawsze idę najprostszą drogą, strasznie nie lubię mieć związanych rąk Oczywiście podałem jej potrzebne twierdzenie, ale obiecałem, że pomyślę nad rozwiązaniem przystępnym dla niej
Z góry dziękuję za wszelką pomoc
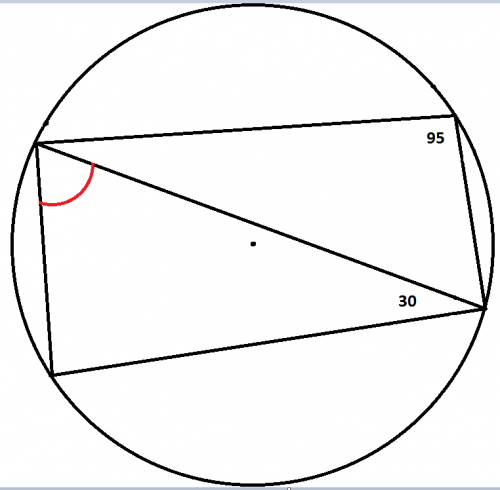
- AU
- f7bf590e84d29f0emed.png (143.97 KiB) Przejrzano 359 razy
Re: Znalezienie miary kąta w okręgu
: 22 wrz 2018, o 23:59
autor: Jan Kraszewski
Można to prosto zrobić korzystając z twierdzenia o kącie środkowym i kącie wpisanym (choć tak naprawdę powtórzymy w ten sposób niejawnie dowód twierdzenia o którym mówisz).
Liczysz miarę kąta środkowego opartego na tym samym łuku co kąt \(\displaystyle{ 95^\circ}\), bierzesz dopełnienie tego kąta do kąta pełnego, a potem liczysz miarę kąta w czworokącie opartego na tym samym łuku, co wspomniane dopełnienie.
JK
Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 00:27
autor: kieubass
Niestety, żadna z cięciw nie przechodzi przez środek okręgu, więc z tego powodu twierdzenie o kącie wpisanym i środkowym od razu odrzuciłem
Zaznaczyłem kropeczką środek okręgu
Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 10:35
autor: janusz47
Zaznaczony na czerwono kąt ma miarę \(\displaystyle{ ?}\)
Z warunku wpisania czworokąta w okrąg:
\(\displaystyle{ | \angle \alpha| +95^{o} = 180^{o}}\)
gdzie: kąt \(\displaystyle{ \alpha}\) leży naprzeciw kąta o mierze \(\displaystyle{ 95^{o}}\) (rysunek).
Stąd
\(\displaystyle{ |\angle \alpha | = 85^{o}}\)
Z trójkąta o kątach:
\(\displaystyle{ 85^{0}, \ \ 30^{o}, \ \ ?}\)
i sumy miar kątów w trójkącie:
\(\displaystyle{ 85^{0} + 30^{o} +? =180^{o}.}\)
Zaznaczony na czerwono kąt ma miarę:
\(\displaystyle{ ? = 180^{o} - 85^{o} - 30^{o}= 65^{o}.}\)
Re: Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 10:53
autor: Longines
janusz47 wyprzedził mnie.
Właśnie pisałem odpowiedź. To jest prawidłowe rozwiązanie zadania.
Re: Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 11:21
autor: Gamma
Jan Kraszewski, podał rozwiązanie, bez użycia tw. o wpisaniu czworokąta w okrąg. Kąt środkowy, o którym mówi, musisz sobie dorysować.
Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 12:35
autor: janusz47
Gamma
Proszę przedstawić to rozwiązanie.
Re: Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 12:40
autor: Gamma
Jan Kraszewski pisze:Można to prosto zrobić korzystając z twierdzenia o kącie środkowym i kącie wpisanym (choć tak naprawdę powtórzymy w ten sposób niejawnie dowód twierdzenia o którym mówisz).
Liczysz miarę kąta środkowego opartego na tym samym łuku co kąt \(\displaystyle{ 95^\circ}\), bierzesz dopełnienie tego kąta do kąta pełnego, a potem liczysz miarę kąta w czworokącie opartego na tym samym łuku, co wspomniane dopełnienie.
JK
No i na koniec wykorzystujemy wiedzę o tym, że suma miar kątów w trójkącie jest równa
\(\displaystyle{ 180 ^\circ}\).
Jasne, powtarzamy dowód twierdzenia, które autor pytania chciał pominąć, ale nie używamy go wprost i myślę że o to autorowi pytania chodziło. To też miałam na myśli pisząc "bez użycia".
Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 14:17
autor: kieubass
janusz47 pisze:Zaznaczony na czerwono kąt ma miarę \(\displaystyle{ ?}\)
Z warunku wpisania czworokąta w okrąg:
\(\displaystyle{ | \angle \alpha| +95^{o} = 180^{o}}\)
gdzie: kąt \(\displaystyle{ \alpha}\) leży naprzeciw kąta o mierze \(\displaystyle{ 95^{o}}\) (rysunek).
Stąd
\(\displaystyle{ |\angle \alpha | = 85^{o}}\)
Z trójkąta o kątach:
\(\displaystyle{ 85^{0}, \ \ 30^{o}, \ \ ?}\)
i sumy miar kątów w trójkącie:
\(\displaystyle{ 85^{0} + 30^{o} +? =180^{o}.}\)
Zaznaczony na czerwono kąt ma miarę:
\(\displaystyle{ ? = 180^{o} - 85^{o} - 30^{o}= 65^{o}.}\)
Chodziło mi o rozwiązanie, BEZ tw. o czworokącie wpisanym w okrąg, bo uczennica jeszcze go nie miała
Re: Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 14:36
autor: Rafsaf
dorysować
\(\displaystyle{ AC}\), potem z równości kątów wpisanych(dwukrotnie) jw
swoją drogą "Bo ja to z geometrii zawsze idę najprostszą drogą" nie za bardzo ma tu zastosowanie, zaryzykuję stwierdzenie że obie metody są równie proste, ta może nawet ciut szybsza
Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 14:46
autor: janusz47
Miara kąta wklęsłego \(\displaystyle{ DOB}\) jest równa \(\displaystyle{ 170^{o}}\)
Miara kąta \(\displaystyle{ BAD}\) jest równa \(\displaystyle{ \frac{1}{2}\cdot 170^{o} = 85^{o}.}\)
Miara kąta czerwonego jest równa \(\displaystyle{ 180^{o} - 85^{o} -30^{o}= 65^{o}.}\)
Jest to zadanie z poziomu rozszerzonego matury, dziwne, że nauczyciel podając zastrzega sobie nie korzystanie z własności miar kątów czworokąta wpisanego w okrąg.
Znalezienie miary kąta w okręgu
: 23 wrz 2018, o 15:50
autor: kieubass
Jest to zadanie z poziomu rozszerzonego matury, dziwne, że nauczyciel podając zastrzega sobie nie korzystanie z własności miar kątów czworokąta wpisanego w okrąg.
Nie do końca, po prostu, to jest zadanie ze strony dajmy na to pięćdziesiątej, a tw. o czworokącie wpisanym w okrąg, ma dopiero na stronie 320 Podałem uczennicy ten sposób "na zaś", ale pytała czy da się zrobić bez tego i wymiękłem -- 23 wrz 2018, o 15:54 --Bardzo dziękuję użytkownikom
Rafsaf i
Janusz47 za pomoc!