Strona 1 z 2
Mój algorytm pseudolosujący
: 10 lip 2017, o 22:50
autor: RafalMajewskiPL
Witam. Najpierw krótki wstęp. Przeglądając algorytmy losujące nie spodobały mi się ich cechy: wylosowane liczby zależały od ilości już wygenerowanych liczb, polegały na liczbach pierwszych lub dawały słabej jakości liczby pseudolosowe. Wtedy przypomniała mi się funkcja Weierstrassa. Po paru edycjach otrzymałem to:
\(\displaystyle{ \sum_{i=0}^{ p_{1} } \sin \left( p_{2}^{i}x \right)}\)
gdzie
\(\displaystyle{ p_{2}}\) nie należy do przedziału
\(\displaystyle{ \left\langle -1,1 \right\rangle}\)
Żeby otrzymać liczbę z przedziału <0,1) wystarczy:
\(\displaystyle{ \sum_{i=0}^{ p_{1} } \left( \sin \left( p_{2}^{i}x \right) \right) -floor \left( \sum_{i=0}^{ p_{1} } \left( \sin \left( p_{2}^{i}x \right) \right) \right)}\)
Im większa wartość
\(\displaystyle{ p_{1}}\) i
\(\displaystyle{ abs \left( p_{2} \right)}\) tym lepiej.
Można uznać za ziarno generatora liczby
\(\displaystyle{ x}\) i
\(\displaystyle{ p_{2}}\).
A teraz jak to wygląda:
(wynik przemnożyłem przez 2 i zastosowałem funkcję floor żeby otrzymać 0 lub 1)
(u góry wynik z mojego algorytmu, a na dole z funkcji random(0,1) z biblioteki math w lua)
\(\displaystyle{ p_{1}=10}\),
\(\displaystyle{ p_{2}=2}\)

- AU
- b1a8b7351e3bab77fb6af315c5dd69a8.png (1.38 KiB) Przejrzano 272 razy
\(\displaystyle{ p_{1}=10}\),
\(\displaystyle{ p_{2}=2.1}\)
(wynik przemnożyłem przez 100 i zastosowałem funkcję floor żeby otrzymać liczbę od 0 do 99)
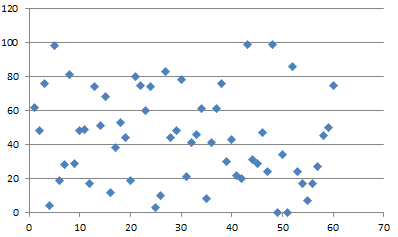
- AU
- 333b5ffb44dc3dd8ffcaa35111bccf84.png (5.47 KiB) Przejrzano 272 razy
Co o tym sądzicie?
Mój algorytm pseudolosujący
: 11 lip 2017, o 09:28
autor: kerajs
Że ilość przeprowadzonych prób jest zbyt mała aby można było coś powiedzieć.
Wygeneruj 100 000 liczb i sprawdź czy każda z możliwych 100 liczb wystąpiła około 1000 razy.
Mój algorytm pseudolosujący
: 11 lip 2017, o 11:08
autor: RafalMajewskiPL
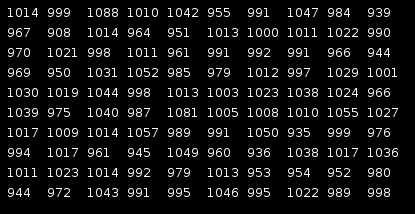
- AU
- de1b6f0c5f5715f9d70e6361930332f1.png (12.06 KiB) Przejrzano 272 razy
Mój algorytm pseudolosujący
: 12 lip 2017, o 18:49
autor: kerajs
Nawet nieźle wyszło, a sądziłem że będzie zdecydowanie gorzej.
Sugerowałbym kilkukrotne powtórzenie tego losowania i sprawdzenie czy największe nadmiary/ niedomiary są przypadkowe/ powtarzają się dla tych samych liczb.
Mój algorytm pseudolosujący
: 12 lip 2017, o 23:48
autor: RafalMajewskiPL
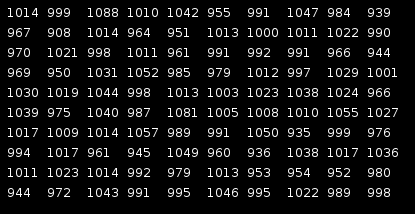
- AU
- de1b6f0c5f5715f9d70e6361930332f1.png (12.06 KiB) Przejrzano 272 razy
\(\displaystyle{ p_{1}=10}\),
\(\displaystyle{ p_{2}=2}\)
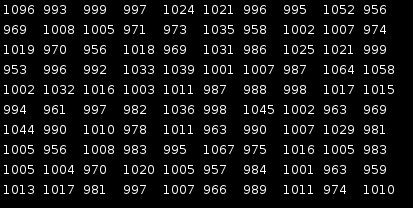
- AU
- c5e6b6d0411dd4e05433e86d27af07bf.png (10.88 KiB) Przejrzano 272 razy
\(\displaystyle{ p_{1}=10}\),
\(\displaystyle{ p_{2}=2.1}\)
- AU
- 24a4eb29ca24e820798d9393cb2af0f2.png (11.3 KiB) Przejrzano 272 razy
\(\displaystyle{ p_{1}=10}\),
\(\displaystyle{ p_{2}=2.5}\)
- AU
- 19628b61b326dca69837664d0dd3c5b0.png (13.35 KiB) Przejrzano 272 razy
\(\displaystyle{ p_{1}=12}\),
\(\displaystyle{ p_{2}=2.3}\)-- 13 lip 2017, o 21:43 --
Mój algorytm pseudolosujący
: 15 lip 2017, o 08:55
autor: kerajs
Co prawda nie o to mi chodziło, ale przy okazji ujawnił się największy problem tych generatorów.
Otrzymywane liczby się powtarzają przy każdej inicjacji generatora, brakuje niezbędnego elementu losowości.
Mój algorytm pseudolosujący
: 17 lip 2017, o 11:10
autor: RafalMajewskiPL
kerajs pisze:Co prawda nie o to mi chodziło, ale przy okazji ujawnił się największy problem tych generatorów.
Otrzymywane liczby się powtarzają przy każdej inicjacji generatora, brakuje niezbędnego elementu losowości.
Oto mi chodziło od początku. Np. jak generujesz szum perlina 1D i chcesz wylosować wartość w danym punkcie to podstawiasz jego pozycję x do wzoru i masz wartość.
Re: Mój algorytm pseudolosujący
: 18 lip 2017, o 10:34
autor: kerajs
A jaki sens w generatorze który przy każdym wznowieniu działania daje identyczne serie wyników?
To tak jakby przy pierwszym rzucie kostką zawsze wypadała 3, a szóstka zawsze była wynikiem w drugim i piątym rzucie.
Re: Mój algorytm pseudolosujący
: 18 lip 2017, o 12:30
autor: RafalMajewskiPL
kerajs pisze:A jaki sens w generatorze który przy każdym wznowieniu działania daje identyczne serie wyników?
To tak jakby przy pierwszym rzucie kostką zawsze wypadała 3, a szóstka zawsze była wynikiem w drugim i piątym rzucie.
No napisałem, że przy generowaniu szumu perlina. Wystarczy zmienić parametr
\(\displaystyle{ p_{2}}\) żeby otrzymać inne wyniki (czyli inny szum).
Re: Mój algorytm pseudolosujący
: 19 lip 2017, o 07:33
autor: kerajs
Nie, nigdzie nie napisałeś że wyniki będą wykorzystywane do generowania szumu.
Na Twoim miejscu sprawdziłbym dodatkowo czy największe odchylenia powtarzają się ilub powiększają się gdy wygenerujesz więcej liczb (np 200 000, 300 000, 500 000, ...). Warto wybrać ten wzór który ma najmniejsze odchyłki.
Re: Mój algorytm pseudolosujący
: 24 lip 2017, o 23:38
autor: RafalMajewskiPL
Chodzi ci o to czy funkcja ma okres?
Re: Mój algorytm pseudolosujący
: 25 lip 2017, o 01:50
autor: kerajs
A dlaczego funkcja? Przecież interesują Cię jedynie uzyskiwane wartości.
Chodzi mi o to, czy przy zwiększeniu ilości wygenerowanych liczb nastąpi wyrównanie ilości wystąpień różnych wyników, zmiana liczb w których są największe rozbieżności od średniej czy może powiększenie się odchyleń w tych liczbach.
Z drugiej strony dla szumu nie ma to większego znaczenia. Przecież szum nie musi być idealnie 'gęsty'.
Re: Mój algorytm pseudolosujący
: 25 lip 2017, o 13:35
autor: RafalMajewskiPL
Podczas programowania programu który mi to pokaże zauważyłem, że mam większe odchylenie standardowe od generatora z biblioteki love.math
EDIT 1: Jest coś takiego jak odchylenie standardowe idealnej zmiennej losowej?
EDIT 2:
Kod: Zaznacz cały
https://www.youtube.com/watch?v=4EtRxG0jY9Y
EDIT 3: Miałem źle ustawiony generator :/
\(\displaystyle{ p_{1}}\) był zamieniony z
\(\displaystyle{ p_{2}}\)
EDIT 4:
Kod: Zaznacz cały
https://www.youtube.com/watch?v=t8DY7ElGGV0
https://www.youtube.com/watch?v=jMC6UphLToY
https://www.youtube.com/watch?v=86v986nFNks
Re: Mój algorytm pseudolosujący
: 28 lip 2017, o 09:37
autor: kerajs
RafalMajewskiPL pisze:Podczas programowania programu który mi to pokaże zauważyłem, że mam większe odchylenie standardowe od generatora z biblioteki love.math
Dla 100 możliwych wyników 9000 losowań jest mała próbą. Zwiększenie ilości prób o jeden rząd może zmienić parametry rozkładu.
RafalMajewskiPL pisze:
EDIT 1: Jest coś takiego jak odchylenie standardowe idealnej zmiennej losowej?
Nie wiem
RafalMajewskiPL pisze:
EDIT 3: Miałem źle ustawiony generator :/
\(\displaystyle{ p_{1}}\) był zamieniony z
\(\displaystyle{ p_{2}}\)
EDIT 4:
Kod: Zaznacz cały
https://www.youtube.com/watch?v=t8DY7ElGGV0
Kod: Zaznacz cały
https://www.youtube.com/watch?v=jMC6UphLToY
https://www.youtube.com/watch?v=86v986nFNks
Oglądnąłem, ale nie napiłeś w jakim celu to pokazujesz.
Mam wrażenie że drepczemy w kółko. Powtórzę to co już napisałem wcześniej:
- Na generator to się nie nadaje ze względu na powtarzalność wyników przy każdej nowej inicjacji algorytmu.
- Na szum się nadaje.
Re: Mój algorytm pseudolosujący
: 28 lip 2017, o 12:30
autor: RafalMajewskiPL
Oglądnąłem, ale nie napiłeś w jakim celu to pokazujesz.
Chciałeś żebym sprawdził czy odchylenia się powtarzają przy zwiększeniu ilości wylosowanych liczb. Można to sprawdzić na filmach.
Na generator to się nie nadaje ze względu na powtarzalność wyników przy każdej nowej inicjacji algorytmu.
Co za problem wziąć czas uniksowy i przekonwertować na liczbę od (mniej więcej) 2 do 4 i wrzucić do
\(\displaystyle{ p_{2}}\)