Strona 1 z 2
Pięciokąty w kwadracie
: 6 sie 2016, o 11:35
autor: kinia7
W kwadracie o boku 10 znajduje się foremny pięciokąt, którego wierzchołki leżą na co najmniej trzech krawędziach kwadratu. Biorąc pod uwagę wszystkie możliwe położenia i wielkości pięciokąta, oblicz jaka część kwadratu nigdy nie zostanie zakryta.
Pięciokąty w kwadracie
: 6 sie 2016, o 12:56
autor: PiotrowskiW
Niech a oznacza nieznaną długość boku pięciokąta foremnego. Wówczas najmniejsza możliwa długość boku kwadratu zawierającego ten wyraża się wzorem \(\displaystyle{ A= \frac{ \sqrt{5}+1 }{2} \cdot a}\) Dlaczego? odsyłam tutaj: [ciach] Mamy zatem \(\displaystyle{ A= 10}\). Wyliczamy z tego małe a, potem korzystamy z gotowego wzoru na pole pięciokąta foremnego i wykonujemy odejmowanie. Tak ja bym to widział. Oczywiście trzeba uzasadnić, ze to co ja napisałem to odpowiedź do tego zadania albo dlaczego to jest źle
Pięciokąty w kwadracie
: 6 sie 2016, o 13:29
autor: kinia7
czyli wg Ciebie \(\displaystyle{ \left( \frac{A}{a} \right)_{min} \approx 1,61803}\)
mnie wychodzi \(\displaystyle{ \left( \frac{A}{a} \right)_{min} \approx 1,59811}\)-- 6 sie 2016, o 13:34 --poza tym nie wystarczy odjąć pole pięciokąta od pola kwadratu, gdyż pięciokąt można cztery razy "przestawić " i za każdym razem zakryje część pola kwadratu niezakrytą w pierwszym położeniu
Pięciokąty w kwadracie
: 6 sie 2016, o 14:06
autor: pesel
kinia7 pisze:Biorąc pod uwagę wszystkie możliwe położenia i wielkości pięciokąta
kinia7 pisze:poza tym nie wystarczy odjąć pole pięciokąta od pola kwadratu, gdyż pięciokąt można cztery razy "przestawić " i za każdym razem zakryje część pola kwadratu niezakrytą w pierwszym położeniu
Wybieram baaaaaardzooooooooooo mały "pięciokącik" i pokrywam nim cały kwadrat przesuwając go po całym kwadracie.
Pięciokąty w kwadracie
: 6 sie 2016, o 14:48
autor: kinia7
pesel pisze:Wybieram baaaaaardzooooooooooo mały "pięciokącik" i pokrywam nim cały kwadrat przesuwając go po całym kwadracie.
wg mnie to jest niemożliwe; zawsze będą baaaaaardzooooooooooo małe narożniki niezakryte
Pięciokąty w kwadracie
: 6 sie 2016, o 20:12
autor: PiotrowskiW
poza tym nie wystarczy odjąć pole pięciokąta od pola kwadratu, gdyż pięciokąt można cztery razy "przestawić " i za każdym razem zakryje część pola kwadratu niezakrytą w pierwszym położeniu
w takim razie inaczej rozumiem treść zadania; wówczas zgadzam się zupełnie z peselem.
Poza tym proszę mi wyjaśnić jak udało ci się wstawić pięciokąt, którego przekątna jest większa od boku kwadratu, w ten kwadrat. Nie umiem sobie tego wyobrazić.
Pięciokąty w kwadracie
: 6 sie 2016, o 20:26
autor: kinia7
PiotrowskiW pisze:w takim razie inaczej rozumiem treść zadania; wówczas zgadzam się zupełnie z peselem.
pesel "pszekąbinował", bo nie da się pokryć całego kwadratu
poza tym jego pomysł nie pasuje już do poprawionej treści zadania
PiotrowskiW pisze:Poza tym proszę mi wyjaśnić jak udało ci się wstawić pięciokąt, którego przekątna jest większa od boku kwadratu, w ten kwadrat. Nie umiem sobie tego wyobrazić.
przekątna pięciokąta jest ociupinę nierównoległa do boku kwadratu
Pięciokąty w kwadracie
: 6 sie 2016, o 20:30
autor: piasek101
Pięciokąt ma być jeden (największy lub najmniejszy z możliwych) - treść ,,foremny pięciokąt".
Pięciokąty w kwadracie
: 6 sie 2016, o 20:55
autor: kinia7
kinia7 pisze:Biorąc pod uwagę wszystkie możliwe położenia i wielkości pięciokąta
ja to rozumiem tak, że pięciokąt można dowolnie zmieniać i przesuwać tak, żeby "pokryć" jak największą część kwadratu
a obliczyć trzeba pole tych części kwadratu, których nie da się zakryć
Pięciokąty w kwadracie
: 6 sie 2016, o 21:10
autor: piasek101
Ale (wg mnie) chodzi o znalezienie najmniejszego i (chociaż niejednoczesne) największego możliwego (spełniającego warunki zadania).
Oczywiście, że możemy ustawiać szukane pięciokąty jak chcemy (warunki zadania) - ale mamy podać te dwa skrajne - możliwie z uzasadnieniem.
Pięciokąty w kwadracie
: 6 sie 2016, o 22:22
autor: kinia7
piasek101 pisze:Ale (wg mnie) chodzi o znalezienie najmniejszego i (chociaż niejednoczesne) największego możliwego (spełniającego warunki zadania).
to akurat nie jest trudne
najmniejszy pięciokąt ma przekątną równą bokowi kwadratu
największy pięciokąt ma bok
\(\displaystyle{ =10\sqrt{2\left(4-\sqrt{2(5+\sqrt5)}\right)}}\)
Pięciokąty w kwadracie
: 6 sie 2016, o 22:27
autor: kerajs
Może pomocne będą obrazki
1)
\(\displaystyle{ a \approx 6,2574}\)

- 2.png (5 KiB) Przejrzano 634 razy
2)
\(\displaystyle{ a \approx 6,18}\)
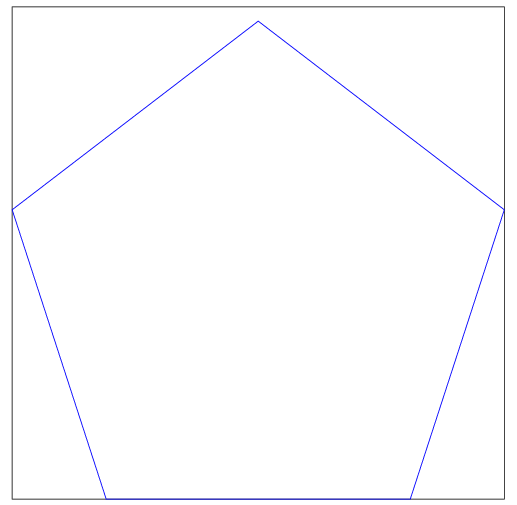
- 3.png (5.03 KiB) Przejrzano 634 razy

- 5.png (12.96 KiB) Przejrzano 634 razy

- 6.png (11.98 KiB) Przejrzano 634 razy

- 7.png (21.31 KiB) Przejrzano 634 razy
Szukane pole będzie trójkątami krzywoliniowymi w czterech rogach kwadratu (wygląda na to że łuki będą tam wypukłe).
Niestety nie wiem jak określić łuki domykające trójkąty i w konsekwencji policzyć szukane pola. Może wystarczy Ci wartość przybliżona?
Pięciokąty w kwadracie
: 6 sie 2016, o 22:38
autor: kinia7
kerajs pisze:Szukane pole będzie trójkątami krzywoliniowymi w czterech rogach kwadratu (wygląda na to że łuki będą tam wypukłe).
Niestety nie wiem jak określić łuki domykające trójkąty i w konsekwencji policzyć szukane pola. Może wystarczy Ci wartość przybliżona?
nie wiem czy wystarczy wartość przybliżona, bo myślę że główny problem polega właśnie na zdefiniowaniu tych łuków
Pięciokąty w kwadracie
: 7 sie 2016, o 12:01
autor: kerajs
Powiększę lewy dolny róg zostawiając tylko wierzchołki pentagonów (niebieskie kropki):
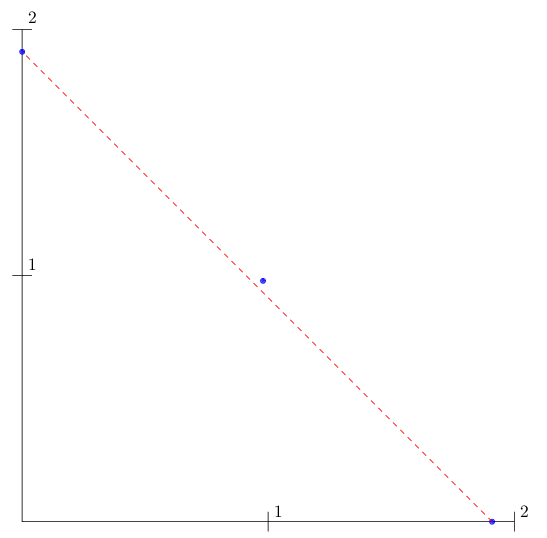
- 1.png (3.85 KiB) Przejrzano 634 razy
Pytałem o rozwiązanie przybliżone bo wierzchołek widoczny na rysunku leży bardzo blisko boku trójkąta (czerwona przerywana linia)
Bok pięciokąta określa wzór:
\(\displaystyle{ a= \frac{10}{\cos (72^o+\beta)+\cos \beta+\cos (72^o+\beta )}}\) dla
\(\displaystyle{ \beta \in \left\langle 0^o;9^o\right\rangle}\)
gdzie beta to kąt między bokiem pentagonu a bokiem kwadratu zawierającym koniec tego boku pentagonu.
Przyjmując że kwadrat jest umieszczony w układzie współrzędnych jak na rysunku (czyli wierzchołek jest
w (0,0) to krzywa wyznaczona przez wierzchołki pentagonu łącząca dolny niebieski wierzchołek ze środkowym ma równanie parametryczne:
\(\displaystyle{ \begin{cases} x= \frac{10 \cos (72^o+\beta)}{\cos (72^o+\beta)+\cos \beta+\cos (72^o+\beta )} \\ y= \frac{10 \sin \beta}{\cos (72^o+\beta)+\cos \beta+\cos (72^o+\beta )} \end{cases}}\) dla
\(\displaystyle{ \beta \in \left\langle 0^o;9^o\right\rangle}\)
Pomoże Ci to w policzeniu pola?
Pięciokąty w kwadracie
: 7 sie 2016, o 19:19
autor: kinia7
`
Na innym forum bb314 (piasek101, pamiętasz ją?) podała wynik:
[link wygasł]
\(\displaystyle{ P_{AEF}=\frac{25}{4}\left(3-\sqrt5\right)\left(4-\sqrt{2\left(5+\sqrt5\right)}\right)}\)