Zgadza się, doszedłem do tych samych wniosków w międzyczasie i wynika z tego np, że jeśli przyjęlibyśmy, że mamy
\(\displaystyle{ 7}\) przycisków i
\(\displaystyle{ 7}\) przyciskową kombinację oraz że naciśnięcie każdego wymaga
\(\displaystyle{ 1}\) sekundy czasu rzeczywistego, to:
Bruteforcem: \(\displaystyle{ 7^7 \cdot 7 \Rightarrow 5764801 [s] = 66,7}\) dnia (tak naprawdę krócej, bo "niechcąco" pewne kombinacje zostaną wciśnięte wcześniej)
Najkrótszym ciągiem: \(\displaystyle{ 7^7 + 7 - 1 \Rightarrow 823549 [s] = 9,5}\) dnia!
Problemem natomiast jest, jaki
dokładnie ten ciąg jest (jedna z możliwości).
Przez ten czas doszedłem do kilku własnych odkryć/wniosków:
Oczywiście w tych wszystkich wywodach kombinacja to dla mnie wariacja z powtórzeniami
Przyjmijmy, że mamy ustaloną liczbę przycisków
\(\displaystyle{ p}\) oraz ustaloną długość kombinacji
\(\displaystyle{ d}\).
Możemy stworzyć pewien graf skierowany, którego wierzchołkami są kolejne możliwe kombinacje długości
\(\displaystyle{ d}\) zawierające cyfry od
\(\displaystyle{ 0}\) do
\(\displaystyle{ p-1}\).
Porządek możemy ustalić w następujący prosty sposób:
\(\displaystyle{ V(G) = [0..p^d-1]}\)
1. Numer wierzchołka odpowiada jego reprezentacji w systemie o podstawie p.
Na przykład dla
\(\displaystyle{ p = 3}\) i
\(\displaystyle{ d = 2}\) wierzchołek o numerze
\(\displaystyle{ 3}\) (indeksujemy od
\(\displaystyle{ 0}\) do
\(\displaystyle{ p^d - 1}\)) odpowiada kombinacji:
\(\displaystyle{ 10}\), czyli czwartej możliwej kombinacji.
\(\displaystyle{ 3_{10}}\) = \(\displaystyle{ 10_3}\)
Czyli myk polega na tym, że za każdym indeksem danego wierzchołka kryje się sekwencja wciśnięć, wystarczy ją "zdekodować".
2. Zbiór krawędzi ustalamy w następujący sposób:
\(\displaystyle{ (v_i,v_j) in E(G) Leftrightarrow j in [(icdot pmod{p^d} ; i cdot pmod{p^d} + p) extcolor{gray}{ wedge i
eq j}}\)
(Ostatnia koniunkcja nie jest potrzebna, bo bez niej relacje są również poprawne dla tego problemu, tyle, że wystąpią w nim wtedy pętle co będzie się trochę kłóciło z dalszymi założeniami)
\(\displaystyle{ |V(G)| = p^d}\)
\(\displaystyle{ |E(G)| = p^{d+1}}\) (bądź
\(\displaystyle{ p^{d+1} - p}\) pomijając pętle)
Z każdego (zaliczając pętle) wychodzi
\(\displaystyle{ p}\) krawędzi oraz wchodzi
\(\displaystyle{ p}\) krawędzi, każdy wierzchołek jest więc stopnia
\(\displaystyle{ 2p}\).
W tej relacji wierzchołków natomiast jest taki myk, że po zdekodowaniu dwóch wierzchołków, które są ze sobą połączone łukiem (w grafie występują także krawędzie, ale mniejsza) możemy zauważyć pewną rzecz:
np. w podanym wyżej przykładzie z wierzchołka
\(\displaystyle{ 0}\) wychodzą
\(\displaystyle{ 3(2)}\) łuki: do
\(\displaystyle{ 0,1,2}\). To co można zauważyć to to, że gdybyśmy usunęli pierwszy bit
\(\displaystyle{ 0}\) i doczepili ostatni bit jednego z tych wierzchołków, to otrzymamy właśnie te wierzchołki po zakodowaniu!
np.
\(\displaystyle{ 0_{10} = 00_3 \Rightarrow 0 \Rightarrow 02_3 = 2_{10}}\)
Czyli za pomocą sekwencji
\(\displaystyle{ 002}\) możemy zminimalizować wpisywanie kombinacji
\(\displaystyle{ 00}\) i
\(\displaystyle{ 02}\) do jedynie
\(\displaystyle{ 3}\)-cyfrowej sekwencji.
Całe sedno problemu sprowadza się więc do jednej rzeczy - znalezienia cyklu/ścieżki Hamiltona.
Gdy znajdziemy taki cykl bądź ścieżkę (bardzo prawdopodobne, że jak już, to są same cykle), reszta jest już bardzo prosta wystarczy z tej sekwencji wierzchołków wydobyć gotową sekwencję wciśnięć, która będzie najkrótszą możliwą.
Zobrazuję to na przykładzie, w którym mamy problem 2 przycisków oraz 3 wciśnięć:
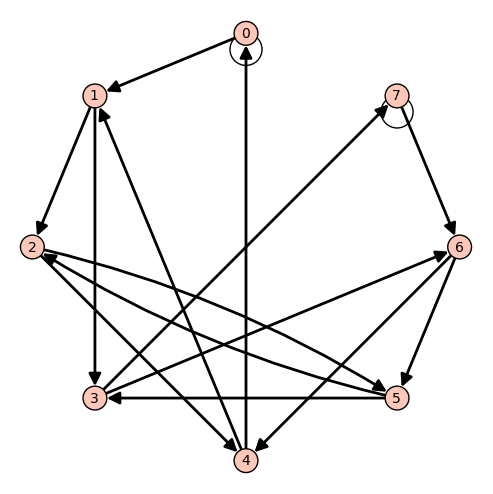
- AU
- Iv8rED7.png (35.43 KiB) Przejrzano 105 razy
Poszukiwania zacząłem od wyboru wierzchołka 0 jako startowego (czy ma to wpływ na znajdywalność? nie wiem/wątpię).
Znalazłem
\(\displaystyle{ 2}\) unikatowe cykle Hamiltona z każdego można wydobyć
\(\displaystyle{ 8}\) różnych sekwencji, czyli w sumie mamy
\(\displaystyle{ 16}\) możliwych sekwencji wciśnięć dla tego problemu, poniżej ilustracje:
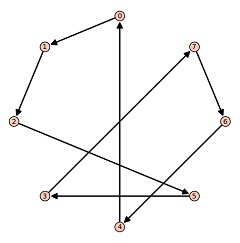
- AU
- tlLiijq.png (10.4 KiB) Przejrzano 105 razy
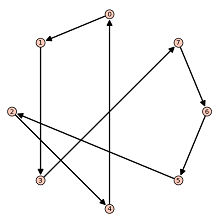
- AU
- juzKKaX.png (9.53 KiB) Przejrzano 105 razy
Wyglądają jak jeden obrócony, odbity cykl.
Warto zwrócić uwagę na niezmienność dwóch podsekwencji: 4,0,1 oraz 3,7,6. Jeśli wystartujemy z 0 to na pewno skończymy na 4.
Tak więc zamiast wciskać:
\(\displaystyle{ 000001010011100\textcolor{gray}{101110111}}\) (tak naprawdę wszystko się zrobi przed szarymi wciśnięciami), czyli wszystkie możliwości po kolei, możemy zastosować minimalną sekwencję odkodowując jeden z cykli Hamiltona w następujący sposób:
\(\displaystyle{ 0,1,2,5,3,7,6,4 \Rightarrow \textcolor{red}{000}, 00\textcolor{red}{1},01\textcolor{red}{0},10\textcolor{red}{1},01\textcolor{red}{1},11\textcolor{red}{1},11\textcolor{red}{0},10\textcolor{red}{0} \Rightarrow \textcolor{red}{0001011100}}\)
Wystarczy że skopiujemy pierwszą kombinację oraz ostatnie bity całej reszty i gotowe!
W ten sposób dostajemy, najkrótszą, najbardziej upakowaną w kombinacje sekwencję dla tego konkretnego problemu (oczywiście istnieje jeszcze 15 innych odmian, ale potrzebujemy do szczęścia tylko jednej).
Wszystko pięknie ale jest mały problem... Najlepiej zobrazuje to ten obrazek:

- AU
- f3MIzyY.png (125.21 KiB) Przejrzano 105 razy
A cóż to jest? Czyżby to był graf dla problemu
\(\displaystyle{ 7}\) przycisków oraz długości równej
\(\displaystyle{ 7}\)?
Bynajmniej, jest to tylko graf marnego problemu
\(\displaystyle{ 3}\) przycisków i długości
\(\displaystyle{ 5}\).
Złożoność problemu rośnie
wykładniczo, jest on ściśle NP-zupełny, oznacza to niezłe kłopoty i może przekreślić szanse na znalezienie chociaż jednego cyklu Hamiltona w problemie
\(\displaystyle{ 7^7}\)
Musiałem trochę poczekać, aż wygeneruje się sam graf problemu
\(\displaystyle{ 3^5}\), nie chcę nawet myśleć o szukaniu cyklu!
I w tym miejscu się zatrzymałem i nie wiem jak dalej ruszyć, program z którego korzystam (Sage) ma wbudowaną funkcję is_hamiltonian, dla wszystkich możliwych do sprawdzenia grafów jakie udało mi się wygenerować zwracała True, więc można się spodziewać, że wszystkie skonstruowane grafy są Hamiltonowskie a to byłby pierwszy sukces, że jest czego szukać.
Niestety są 2 problemy.
Dla grafów skierowanych funkcja nie może zwrócić sekwencji wierzchołków, mimo znalezienia cyklu, ale to mniejszy problem.
Drugim problemem jest złożoność, od 20~30 wierzchołków zaczynają się problemy czasowe, powyższy graf
\(\displaystyle{ f(3,5)}\) (tak go chyba nazwę, graf fezowski ) ma wierzchołków 243! a graf
\(\displaystyle{ f(7,7)}\)...
823543!!!
Nie ma więc najmniejszej szansy na znalezienie cykli drogą algorytmiczną. Pocieszający może być fakt, że przy tak wielkich liczbach graf jest śmiesznie rzadki (nowa definicja ) w porównaniu do kwadratu wierzchołków.
Jedyną nadzieją pozostaje szybkie odczytanie sekwencji opierając się na własnościach tego grafu, znalezieniu jakichś zależności jak np. te które podałem wyżej. Patrząc na wielkość grafu można się spodziewać, że ostatecznych cykli może być mnóstwo, tylko jak je znaleźć?
Być może ktoś spotkał się z podobnym problemem, podobnym bądź tak samo zdefiniowanym grafem, do którego są już jakiegoś typu gotowce, wzory?
Byłbym wdzięczny za wszelką pomoc, bądź własne przemyślenia na ten temat
Pozdrawiam

