KPR pisze:1.
Ponieważ obrazem zbioru
\(\displaystyle{ \mathbb R}\) w funkcji
\(\displaystyle{ f}\) jest przedział
\(\displaystyle{ \langle 0, +\infty)}\), to dla każdego
\(\displaystyle{ a \in \langle 0, +\infty)}\) istnieje takie
\(\displaystyle{ x \in \mathbb R}\) takie, że
\(\displaystyle{ f(x)=a}\). Wtedy, zgodnie z warunkami zadania mamy
\(\displaystyle{ f(a)=f(f(x))=f(x)=a}\). Ponieważ
\(\displaystyle{ a}\) jest dowolną liczbą nieujemną, to dla dowolnego
\(\displaystyle{ x \in \langle 0, +\infty)}\) zachodzi
\(\displaystyle{ f(x)=x}\).
Niech teraz
\(\displaystyle{ x}\) będzie liczbą ujemną. Wtedy z warunków zadania mamy
\(\displaystyle{ f(x)=f(-x)=-x}\), ponieważ wtedy
\(\displaystyle{ -x \in \langle 0, +\infty)}\).
Otrzymujemy zatem, że dla
\(\displaystyle{ x \ge 0}\)\(\displaystyle{ f(x)=x}\), a dla
\(\displaystyle{ x < 0}\)\(\displaystyle{ f(x)=-x}\). Zatem
\(\displaystyle{ f(x)=|x|}\). Funkcja ta spełnia warunki zadania.
Odpowiedź. Jedyną funkcją spełniającą warunki zadania jest
\(\displaystyle{ f(x)=|x|}\).
2.
Lemat.
Jeśli
\(\displaystyle{ x}\),
\(\displaystyle{ y}\),
\(\displaystyle{ z}\) są takimi liczbami rzeczywistymi, że
\(\displaystyle{ x+y+z=0}\), to
\(\displaystyle{ \frac{(x^2+y^2+z^2)^2(x^3+y^3+z^3)}{12}= \frac{x^7+y^7+z^7}{7}}\).
Dowód.
Z warunków lematu wynika, że
\(\displaystyle{ z=-x-y}\). Zatem
\(\displaystyle{ \frac{(x^2+y^2+z^2)^2(x^3+y^3+z^3)}{12}= \frac{(x^2+y^2+x^2+2xy+y^2)^2(x^3+y^3-x^3-3x^2y-3xy^2-y^3)}{12}=\frac{(2x^2+2y^2+2xy)^2(-3x^2y-3xy^2)}{12}=(x^2+y^2+xy)^2(-x^2y-xy^2)=-(x^2+y^2+xy)(x^4y+x^2y^3+x^3y^2+x^3y^2+xy^4+x^2y^3)=-(x^2+y^2+xy)(x^4y+2x^2y^3+2x^3y^2+xy^4)=-(x^6y+2x^4y^3+2x^5y^2+x^3y^4+x^4y^3+2x^2y^5+2x^3y^4+xy^6+x^5y^2+2x^3y^4+2x^4y^3+x^2y^5)=-(x^6y+3x^2y^5+5x^3y^4+5x^4y^3+3x^5y^2+x^6y)= \frac{x^7+y^7-(x^7+7x^6y+21x^2y^5+35x^3y^4+35x^4y^3+21x^5y^2+7x^6y+y^7)}{7}= \frac{x^7+y^7+(-x-y)^7}{7}= \frac{x^7+y^7+z^7}{7}}\), co kończy dowód lematu.
Załóżmy, że liczby
\(\displaystyle{ x}\),
\(\displaystyle{ y}\),
\(\displaystyle{ z}\) spełniają dany układ równań. Wtedy, na mocy lematu
\(\displaystyle{ \frac{18(x^2+y^2+z^2)^2}{12}= 294}\), skąd
\(\displaystyle{ (x^2+y^2+z^2)^2= 294 \cdot \frac{2}{3}=196}\). Zatem
\(\displaystyle{ x^2+y^2+z^2=14}\) (ponieważ jest to liczba nieujemna, to nie może być równa -14).
Przypuśćmy, że dwie spośród liczb
\(\displaystyle{ x}\),
\(\displaystyle{ y}\),
\(\displaystyle{ z}\) są równe. Załóżmy bez straty ogólności, że są to
\(\displaystyle{ y}\) i
\(\displaystyle{ z}\). Wtedy mamy
\(\displaystyle{ \begin{cases}x+2y=0 \\ x^2+2y^2=14\end{cases}}\).
Podstawiając do drugiego równania
\(\displaystyle{ x=-2y}\) otrzymujemy
\(\displaystyle{ 6y^2=14}\), skąd
\(\displaystyle{ y= \pm \sqrt{ \frac{7}{3} }}\) i po podstawieniu do
\(\displaystyle{ x=-2y}\) \(\displaystyle{ x= \mp 2\sqrt{ \frac{7}{3} }}\). Zatem
\(\displaystyle{ x^3+y^3+z^3=x^3+2y^3= \mp 8 \cdot \frac{7}{3}\sqrt{\frac{7}{3}} \pm 2 \cdot \frac{7}{3}\sqrt{\frac{7}{3}} =\mp 6 \cdot \frac{7}{3}\sqrt{\frac{7}{3}} \neq 18}\). Doszliśmy do sprzeczności, zatem wszystkie liczby
x,
y,
z są różne.
Ponieważ
\(\displaystyle{ z=-x-y}\), to
\(\displaystyle{ x^2+y^2+z^2=x^2+y^2+x^2+2xy+y^2=2x^2+2y^2+2xy}\). Zatem z równości
\(\displaystyle{ x^2+y^2+z^2=14}\) wynika
\(\displaystyle{ y^2+xy+x^2-7=0}\). Analogicznie
\(\displaystyle{ z^2+xz+x^2-7=0}\). Zatem
\(\displaystyle{ y}\) i
\(\displaystyle{ z}\) są różnymi (jak pokazaliśmy wcześniej) pierwiastkami wielomianu
\(\displaystyle{ a^2-ax+x^2-7}\) (z niewiadomą
\(\displaystyle{ a}\)). Zatem ze wzorów Viete'a
\(\displaystyle{ x^3+y^3+z^3=(-y-z)^3+y^3+z^3=-y^3-3y^2z-3yz^2-3z^3+y^3+z^3=-3y^2z-3yz^2=-3yz(y+z)=-3(x^2-7)(-x)=3(x^3-7x)}\).
Zatem
\(\displaystyle{ 3(x^3-7x)=18}\), zatem
\(\displaystyle{ x^3-7x-6=0}\). Można sprawdzić, że rozwiązaniami tego równania są liczby 3, -2 i -1, a ponieważ jest ono stopnia trzeciego, to ma co najwyżej 3 rozwiązania. Zatem
\(\displaystyle{ x}\) jest równe 3, -2 lub -1. Analogicznie
\(\displaystyle{ y}\) oraz
\(\displaystyle{ z}\) są obie równe 3, -2 lub -1. Ponieważ jednak liczby
\(\displaystyle{ x}\),
\(\displaystyle{ y}\),
\(\displaystyle{ z}\) są różne, to jedna z nich jest równa 3, jedna jest równa -2, a jedna jest równa -1. Jak łatwo sprawdzić, liczby te są rozwiązaniami wyjściowego układu równań (w dowolnej konfiguracji, ze względu na symetryczność układu).
Odpowiedź. Wszystkimi rozwiązaniami danego układu równań są trójki (3,-2,-1),(3,-1,-2),(-2,3,-1),(-2,-1,3),(-1,3,-2),(-1,-2,3).
3.
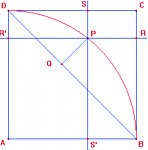
- AU
- dbecb1cbeccf05edm.jpg (5.61 KiB) Przejrzano 917 razy
Niech R' oznacza punkt przecięcia prostych PR i AD, a S' niech oznacza punkt przecięcia prostych PS i AB. Oznaczmy |DQ|=
x i |AB|=
a. Wtedy, ponieważ
\(\displaystyle{ \angle DQP=\angle DSP=90 ^ \circ}\), to z twierdzenia Pitagorasa
\(\displaystyle{ x^2+PQ^2=PD^2=PS^2+DS^2=PS^2+R'P^2=PS^2+(a-PR)^2=PS^2+a^2-2aPR+PR^2}\).
Analogicznie, ponieważ
\(\displaystyle{ \angle BQP=\angle BRP=90 ^ \circ}\), to z twierdzenia Pitagorasa mamy
\(\displaystyle{ BQ^2+PQ^2=PR^2+(a-PS)^2}\), czyli
\(\displaystyle{ (a\sqrt 2-x)^2+PQ^2=PR^2+a^2-2aPS+PS^2}\).
Mamy zatem następujący układ równości:
\(\displaystyle{ \begin{cases}x^2+PQ^2=PS^2+a^2-2aPR+PR^2 \\ 2a^2-2ax\sqrt2+x^2+PQ^2=PR^2+a^2-2aPS+PS^2\end{cases}}\).
Odejmijmy je stronami. Otrzymujemy
\(\displaystyle{ 2ax\sqrt2-2a^2=2aPS-2aPR |:2a}\)
\(\displaystyle{ a-x\sqrt2=PR-PS}\) (1)
Teraz dodajmy je stronami. Otrzymujemy
\(\displaystyle{ 2x^2+2a^2-2ax\sqrt 2+2PQ^2=PS^2+PR^2+(a-PR)^2+(a-PS)^2}\). Zauważmy, że
\(\displaystyle{ a-PR=PR'=S'A}\) i
\(\displaystyle{ a-PS=PS'}\). Z twierdzenia Pitagorasa mamy zatem
\(\displaystyle{ (a-PR)^2+(a-PS)^2=S'A^2+PS'^2=AP^2=a^2}\). Zatem równość przyjmuje postać
\(\displaystyle{ 2x^2+2a^2-2ax\sqrt 2+2PQ^2=PS^2+PR^2+a^2}\)
Przekształcając ją otrzymujemy
\(\displaystyle{ 2x^2+a^2-2ax\sqrt 2+2PQ^2=PS^2+PR^2}\)
\(\displaystyle{ (a-x\sqrt2)^2+2PQ^2=PS^2+PR^2}\).
Stąd i z (1) mamy
\(\displaystyle{ (PR-PS)^2+2PQ^2=PS^2+PR^2}\)
\(\displaystyle{ PR^2+PS^2-2PS \cdot PR+2PQ^2=PS^2+PR^2}\)
\(\displaystyle{ -2PS \cdot PR+2PQ^2=0}\)
\(\displaystyle{ PS \cdot PR=PQ^2}\), c.n.d.
4.
Zauważmy, że zachodzi jedna z nierówności
\(\displaystyle{ ab \le 1}\),
\(\displaystyle{ cd \le 1}\). Istotnie, w przeciwnym wypadku mielibyśmy
\(\displaystyle{ ab>1}\) i
\(\displaystyle{ cd>1}\), co po wymnożeniu daje
\(\displaystyle{ abcd>1}\), co jest sprzeczne z warunkami zadania.
Załóżmy bez straty ogólności, że
\(\displaystyle{ ab \le 1}\). Wtedy
\(\displaystyle{ b \le \frac{1}{a}}\), skąd
\(\displaystyle{ \frac{1}{1+a}+ \frac{1}{1+b} \ge \frac{1}{1+a}+ \frac{1}{1+ \frac{1}{a} }=\frac{1}{1+a}+ \frac{a}{a+1}=1}\). Ponadto, ponieważ
\(\displaystyle{ c,d>0}\), to
\(\displaystyle{ \frac{1}{1+c},\frac{1}{1+d}>0}\). Zatem
\(\displaystyle{ \frac{1}{1+a}+ \frac{1}{1+b}+\frac{1}{1+c}+ \frac{1}{1+d}>\frac{1}{1+a}+ \frac{1}{1+b} \ge 1}\).
Zatem
\(\displaystyle{ t=1}\) spełnia warunki zadania.
Podstawmy
\(\displaystyle{ a,b,c=n , d= \frac{1}{n^3}}\), gdzie
\(\displaystyle{ n \in \mathbb N}\). Wtedy
\(\displaystyle{ \frac{1}{1+a}+ \frac{1}{1+b}+\frac{1}{1+c}+ \frac{1}{1+d}= \frac{3}{1+n}+ \frac{1}{1+ \frac{1}{n^3} }=\frac{3}{1+n}+ \frac{n^3}{n^3+ 1}= \frac{3(n^2-n+1)}{n^3+1} +\frac{n^3}{n^3+ 1}= \frac{n^3+3n^2-3n+3}{n^3+1}=\frac{1+ \frac{3}{n} - \frac{3}{n^2} + \frac{3}{n^3}}{1+ \frac{1}{n^3} }}\).
Ponieważ
\(\displaystyle{ \lim_{n \to \infty} \frac{1}{n}=0}\),
\(\displaystyle{ \lim_{n \to \infty} \frac{1}{n^2}=0}\),
\(\displaystyle{ \lim_{n \to \infty} \frac{1}{n^3}=0}\), to ze wzoru na sumę oraz iloraz granic
\(\displaystyle{ \lim_{n \to\infty }\frac{1+ \frac{3}{n} - \frac{3}{n^2} + \frac{3}{n^3}}{1+ \frac{1}{n^3} }= \frac{1+0+0+0}{1+0}=1}\). Zatem dla dowolnej liczby
\(\displaystyle{ t_1}\) większej od 1 istnieje takie
\(\displaystyle{ n}\), że dla
\(\displaystyle{ a,b,c=n , d= \frac{1}{n^3}}\) zachodzi
\(\displaystyle{ \frac{1}{1+a}+ \frac{1}{1+b}+\frac{1}{1+c}+ \frac{1}{1+d}<t_1}\). Zatem żadna liczba rzeczywista większa od 1 nie należy do zbioru dodatnich
\(\displaystyle{ t}\) spełniających
\(\displaystyle{ \frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}+\frac{1}{1+d}>t}\) dla dowolnych
\(\displaystyle{ a,b,c,d>0}\) takich, że
\(\displaystyle{ abcd=1}\). Liczba 1 jest zatem największym elementem tego zbioru.
5.
Zauważmy najpierw, że dla każdej liczby
\(\displaystyle{ n \neq 10}\) warunki zadania spełnia liczba A, która ma
\(\displaystyle{ \left\lceil \frac{n}{9} \right\rceil}\) cyfr, z czego
\(\displaystyle{ \left\lceil \frac{n}{9} \right\rceil-1}\) ostatnich jest dziewiątkami, a pierwsza jej cyfra wynosi
\(\displaystyle{ n-9\left(\left\lceil \frac{n}{9} \right\rceil-1 \right)}\). Istotnie, wtedy dla każdej liczby naturalnej
\(\displaystyle{ k}\) mniejszej od
\(\displaystyle{ A}\) każda cyfra liczby
\(\displaystyle{ k}\) jest nie większa od znajdującej się na tej samej pozycji (licząc od prawej strony) cyfry liczby
\(\displaystyle{ A}\). Zatem przy odejmowaniu pisemnym liczby
\(\displaystyle{ k}\) od liczby
\(\displaystyle{ A}\) żadna liczba nie zostanie przeniesiona do "pamięci" (ponieważ robi się to tylko wtedy, gdy cyfra odjemnika jest mniejsza od odpowiedniej cyfry odjemnej). Oznacza to, że każda cyfra różnicy będzie różnicą cyfry odjemnej znajdującej się na tej samej pozycji (licząc od prawej strony) i cyfry odjemnika znajdującej się na tej samej pozycji. Jeśli równość tę zsumujemy po wszystkich pozycjach cyfr, to otrzymamy, że suma cyfr różnicy
\(\displaystyle{ A-k}\) jest równa różnicy sumy cyfr odjemnej, czyli
\(\displaystyle{ A}\) i sumy cyfr odjemnika, czyli
\(\displaystyle{ k}\). Zachodzi zatem
\(\displaystyle{ S(k)+S(A-k)=S(A)=9\left(\left\lceil \frac{n}{9} \right\rceil-1\right)+n-9\left(\left\lceil \frac{n}{9} \right\rceil-1 \right)=n}\). Zatem taka liczba
\(\displaystyle{ A}\) spełnia warunki zadania.
Załóżmy teraz, że dane są takie liczby
\(\displaystyle{ A}\) i
\(\displaystyle{ n}\), które spełniają warunki zadania.
Udowodnimy najpierw, że
\(\displaystyle{ S(A)=n}\).
Zauważmy, że
\(\displaystyle{ A}\) nie może być potęgą liczby 10. Gdyby tak było, to byłoby ono potęgą o wykładniku większym niż 1, ponieważ liczba A równa 1 lub 10 nie spełnia warunków zadania dla żadnego
\(\displaystyle{ n \neq 10}\). Wtedy mielibyśmy
\(\displaystyle{ S(A-10)+S(10)=n=S(A-1)+S(1)}\), a ponieważ wtedy ostatnia cyfra liczby
\(\displaystyle{ A-10}\) byłaby równa 0, to mielibyśmy
\(\displaystyle{ S(A-10)+9=S(A-1)}\), zatem po podstawieniu
\(\displaystyle{ S(A-10)+S(10)=S(A-10)+9+S(1)}\). Po skróceniu otrzymalibyśmy
\(\displaystyle{ S(10)=9+S(1)}\), czyli
\(\displaystyle{ 1=10}\), co jest sprzecznością. Zatem
\(\displaystyle{ A}\) nie jest potęgą liczby 10.
Niech
\(\displaystyle{ m}\) oznacza liczbę cyfr liczby
\(\displaystyle{ A}\). Rozważmy liczbę
\(\displaystyle{ A-10^{m-1}}\). Ponieważ
m-ta od prawej strony cyfra liczby
\(\displaystyle{ A}\) jest jej pierwszą cyfrą, to jest różna od 0. Zatem odjęcie od liczby
\(\displaystyle{ A}\) liczby
\(\displaystyle{ 10^{m-1}}\) spowoduje zmniejszenie tej cyfry o 1, a pozostałe cyfry pozostaną po takim odjęciu bez zmian. Zatem
\(\displaystyle{ S(A-10^{m-1})=S(A)-1}\). Poza tym ponieważ
\(\displaystyle{ A}\) nie jest potęga liczby 10, to
\(\displaystyle{ 10^{m-1}<A}\), zatem z warunków zadania mamy
\(\displaystyle{ n=S(10^{m-1})+S(A-10^{m-1})=1+S(A)-1=S(A)}\).
Oznaczmy przez
\(\displaystyle{ B}\) najmniejszą liczbę naturalną o sumie cyfr równej
\(\displaystyle{ n}\). Zauważmy teraz, że jeśli
\(\displaystyle{ A>B}\), to
\(\displaystyle{ S(A-B)+S(B)=n}\). Zatem
\(\displaystyle{ S(A-B)=0}\), co jest sprzeczne z tym, że
\(\displaystyle{ A>B}\). Zatem jeśli liczby
\(\displaystyle{ A}\) i
\(\displaystyle{ n}\) spełniają warunki zadania, to
\(\displaystyle{ A}\) jest najmniejszą liczbą naturalną o sumie cyfr równej
\(\displaystyle{ n}\). Zatem dla danej liczby
\(\displaystyle{ n \neq 10}\) istnieje maksymalnie jedna liczba
\(\displaystyle{ A}\) spełniająca warunki zadania. Ponieważ, jak pokazaliśmy na początku, dla każdego
\(\displaystyle{ n \neq 10}\) istnieje co najmniej jedna taka liczba, to istnieje dokładnie jedna taka liczba, c.n.d.

